The #P-complete problems form a complexity class in computational complexity theory. The problems in this complexity class are defined by having the following two properties:
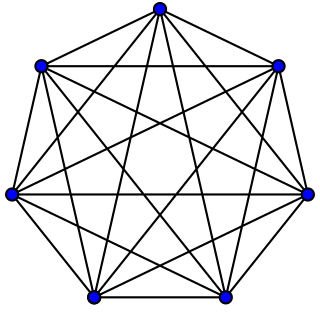
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In the mathematical discipline of graph theory, a matching or independent edge set in an undirected graph is a set of edges without common vertices. Finding a matching in a bipartite graph can be treated as a network flow problem.

In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.

The chromatic polynomial is a graph polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to study the four color problem. It was generalised to the Tutte polynomial by Hassler Whitney and W. T. Tutte, linking it to the Potts model of statistical physics.

In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.

The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a graph polynomial. It is a polynomial in two variables which plays an important role in graph theory. It is defined for every undirected graph and contains information about how the graph is connected. It is denoted by .
In the fields of chemical graph theory, molecular topology, and mathematical chemistry, a topological index also known as a connectivity index is a type of a molecular descriptor that is calculated based on the molecular graph of a chemical compound. Topological indices are numerical parameters of a graph which characterize its topology and are usually graph invariant. Topological indices are used for example in the development of quantitative structure-activity relationships (QSARs) in which the biological activity or other properties of molecules are correlated with their chemical structure.
Haruo Hosoya is a Japanese chemist and emeritus professor of Ochanomizu University, Tokyo, Japan. He is the namesake of the Hosoya index used in discrete mathematics and computational chemistry.
In chemical graph theory, the Wiener index introduced by Harry Wiener, is a topological index of a molecule, defined as the sum of the lengths of the shortest paths between all pairs of vertices in the chemical graph representing the non-hydrogen atoms in the molecule.
In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems.

In the mathematical field of graph theory, the ladder graphLn is a planar, undirected graph with 2n vertices and 3n – 2 edges.
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.
In the mathematical fields of graph theory and combinatorics, a matching polynomial is a generating function of the numbers of matchings of various sizes in a graph. It is one of several graph polynomials studied in algebraic graph theory.
The FKT algorithm, named after Fisher, Kasteleyn, and Temperley, counts the number of perfect matchings in a planar graph in polynomial time. This same task is #P-complete for general graphs. For matchings that are not required to be perfect, counting them remains #P-complete even for planar graphs. The key idea of the FKT algorithm is to convert the problem into a Pfaffian computation of a skew-symmetric matrix derived from a planar embedding of the graph. The Pfaffian of this matrix is then computed efficiently using standard determinant algorithms.

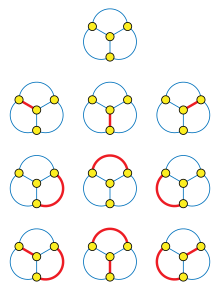
In mathematics, the telephone numbers or the involution numbers form a sequence of integers that count the ways n telephone lines can be connected to each other, where each line can be connected to at most one other line. These numbers also describe the number of matchings of a complete graph on n vertices, the number of permutations on n elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with n cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values
In graph theory, an induced matching or strong matching is a subset of the edges of an undirected graph that do not share any vertices and includes every edge connecting any two vertices in the subset.