In mathematical order theory, an ideal is a special subset of a partially ordered set (poset). Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion. Ideals are of great importance for many constructions in order and lattice theory.
George Yuri Rainich (Rabinovich) (March 25, 1886 in Odessa – October 10, 1968) was a leading mathematical physicist in the early twentieth century.
Michio Suzuki was a Japanese mathematician who studied group theory.
Abraham Adrian Albert was an American mathematician. In 1939, he received the American Mathematical Society's Cole Prize in Algebra for his work on Riemann matrices. He is best known for his work on the Albert–Brauer–Hasse–Noether theorem on finite-dimensional division algebras over number fields and as the developer of Albert algebras, which are also known as exceptional Jordan algebras.

Phillip Augustus Griffiths IV is an American mathematician, known for his work in the field of geometry, and in particular for the complex manifold approach to algebraic geometry. He is a major developer in particular of the theory of variation of Hodge structure in Hodge theory and moduli theory, which forms part of transcendental algebraic geometry and which also touches upon major and distant areas of differential geometry. He also worked on partial differential equations, coauthored with Shiing-Shen Chern, Robert Bryant and Robert Gardner on Exterior Differential Systems.
The monster vertex algebra is a vertex algebra acted on by the monster group that was constructed by Igor Frenkel, James Lepowsky, and Arne Meurman. R. Borcherds used it to prove the monstrous moonshine conjectures, by applying the Goddard–Thorn theorem of string theory to construct the monster Lie algebra, an infinite-dimensional generalized Kac–Moody algebra acted on by the monster.
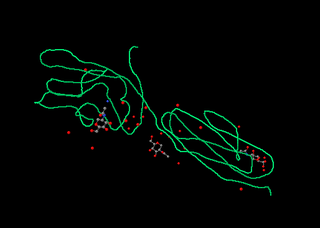
CD2 is a cell adhesion molecule found on the surface of T cells and natural killer (NK) cells. It has also been called T-cell surface antigen T11/Leu-5, LFA-2, LFA-3 receptor, erythrocyte receptor and rosette receptor.
In mathematics, L2 cohomology is a cohomology theory for smooth non-compact manifolds M with Riemannian metric. It is defined in the same way as de Rham cohomology except that one uses square-integrable differential forms. The notion of square-integrability makes sense because the metric on M gives rise to a norm on differential forms and a volume form.
Eliezer 'Leon' Ehrenpreis was a mathematician at Temple University who proved the Malgrange–Ehrenpreis theorem, the fundamental theorem about differential operators with constant coefficients. He previously held tenured positions at Yeshiva University and at the Courant Institute at New York University.
The enzyme lipid-phosphate phosphatase (EC 3.1.3.76) catalyzes the reaction
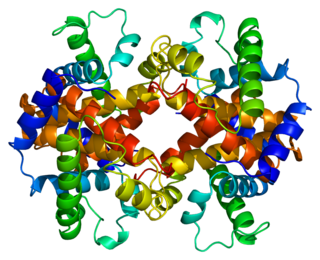
Hemoglobin subunit epsilon is a protein that in humans is encoded by the HBE1 gene.

Alkaline phosphatase, placental type also known as placental alkaline phosphatase (PLAP) is an allosteric enzyme that in humans is encoded by the ALPP gene.

2-Aminopurine, a purine analog of guanine and adenine, is a fluorescent molecular marker used in nucleic acid research. It most commonly pairs with thymine as an adenine-analogue, but can also pair with cytosine as a guanine-analogue. For this reason it is sometimes used in the laboratory for mutagenesis.
In the mathematical field of algebraic geometry, purity is a theme covering a number of results and conjectures, which collectively address the question of proving that "when something happens, it happens in a particular codimension".

Richard Vincent Kadison was an American mathematician known for his contributions to the study of operator algebras.
James Dugundji was an American mathematician, a professor of mathematics at the University of Southern California.
Friederich Ignaz Mautner was an Austrian-American mathematician, known for his research on the representation theory of groups, functional analysis, and differential geometry. He is known for Mautner's Lemma and Mautner's Phenomenon in the representation theory of Lie groups.

Alfred Leon Foster (1904-1994) was an American mathematician. He was a professor at the University of California, Berkeley, from 1934 until 1971. In 1932, he was an Invited Speaker at the ICM in Zürich.
Maurice Haskell Heins was an American mathematician, specializing in complex analysis and harmonic analysis.
Local rigidity theorems in the theory of discrete subgroups of Lie groups are results which show that small deformations of certain such subgroups are always trivial. It is different from Mostow rigidity and weaker than superrigidity.







