In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.
In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,5}. It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from "tetrahedral complex") and a polytetrahedron, being bounded by tetrahedral cells.
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {5,3,3}. It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hecatonicosachoron, dodecacontachoron and hecatonicosahedroid.
In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.
In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices. One can build it from the 600-cell by diminishing a select subset of icosahedral pyramids and leaving only their icosahedral bases, thereby removing 480 tetrahedra and replacing them with 24 icosahedra.
In hyperbolic geometry, the order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.
In geometry, the icosahedral honeycomb is one of four compact, regular, space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {3,5,3}, there are three icosahedra around each edge, and 12 icosahedra around each vertex, in a regular dodecahedral vertex figure.
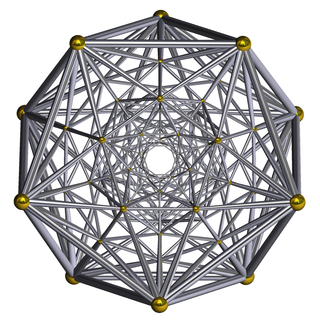
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polytope, discovered in 1965 by Conway and Guy. Topologically, under its highest symmetry, the pentagonal antiprisms have D5d symmetry and there are two types of tetrahedra, one with S4 symmetry and one with Cs symmetry.
In geometry, a truncated 120-cell is a uniform 4-polytope formed as the truncation of the regular 120-cell.
In hyperbolic geometry, a uniform honeycomb in hyperbolic space is a uniform tessellation of uniform polyhedral cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by permutations of rings of the Coxeter diagrams for each family.
In geometry, a pentagonal polytope is a regular polytope in n dimensions constructed from the Hn Coxeter group. The family was named by H. S. M. Coxeter, because the two-dimensional pentagonal polytope is a pentagon. It can be named by its Schläfli symbol as {5, 3n − 2} (dodecahedral) or {3n − 2, 5} (icosahedral).
In the field of hyperbolic geometry, the order-5 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere, a flat plane in hyperbolic space that approaches a single ideal point at infinity.
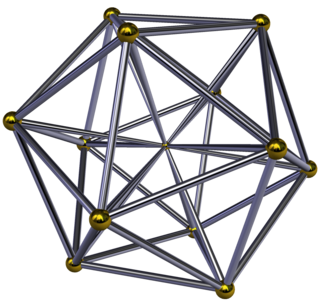
The icosahedral pyramid is a four-dimensional convex polytope, bounded by one icosahedron as its base and by 20 triangular pyramid cells which meet at its apex. Since an icosahedron's circumradius is less than its edge length, the tetrahedral pyramids can be made with regular faces.
In geometry, a Blind polytope is a convex polytope composed of regular polytope facets. The category was named after the German couple Gerd and Roswitha Blind, who described them in a series of papers beginning in 1979. It generalizes the set of semiregular polyhedra and Johnson solids to higher dimensions.
In 4-dimensional geometry, the tetrahedral bipyramid is the direct sum of a tetrahedron and a segment, {3,3} + { }. Each face of a central tetrahedron is attached with two tetrahedra, creating 8 tetrahedral cells, 16 triangular faces, 14 edges, and 6 vertices. A tetrahedral bipyramid can be seen as two tetrahedral pyramids augmented together at their base.
