
In logic, a logical connective is a logical constant used to connect two or more formulas. For instance in the syntax of propositional logic, the binary connective can be used to join the two atomic formulas and , rendering the complex formula .
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of sample data. A statistical model represents, often in considerably idealized form, the data-generating process.
In psychometrics, item response theory (IRT) is a paradigm for the design, analysis, and scoring of tests, questionnaires, and similar instruments measuring abilities, attitudes, or other variables. It is a theory of testing based on the relationship between individuals' performances on a test item and the test takers' levels of performance on an overall measure of the ability that item was designed to measure. Several different statistical models are used to represent both item and test taker characteristics. Unlike simpler alternatives for creating scales and evaluating questionnaire responses, it does not assume that each item is equally difficult. This distinguishes IRT from, for instance, Likert scaling, in which "All items are assumed to be replications of each other or in other words items are considered to be parallel instruments" (p. 197). By contrast, item response theory treats the difficulty of each item as information to be incorporated in scaling items.

Association rule learning is a rule-based machine learning method for discovering interesting relations between variables in large databases. It is intended to identify strong rules discovered in databases using some measures of interestingness.
In mathematical logic and computer science, the calculus of constructions (CoC) is a type theory created by Thierry Coquand. It can serve as both a typed programming language and as constructive foundation for mathematics. For this second reason, the CoC and its variants have been the basis for Coq and other proof assistants.

The material conditional is an operation commonly used in logic. When the conditional symbol is interpreted as material implication, a formula is true unless is true and is false. Material implication can also be characterized inferentially by modus ponens, modus tollens, conditional proof, and classical reductio ad absurdum.
Latent semantic analysis (LSA) is a technique in natural language processing, in particular distributional semantics, of analyzing relationships between a set of documents and the terms they contain by producing a set of concepts related to the documents and terms. LSA assumes that words that are close in meaning will occur in similar pieces of text. A matrix containing word counts per document is constructed from a large piece of text and a mathematical technique called singular value decomposition (SVD) is used to reduce the number of rows while preserving the similarity structure among columns. Documents are then compared by taking the cosine of the angle between the two vectors formed by any two columns. Values close to 1 represent very similar documents while values close to 0 represent very dissimilar documents.

In mathematics, a Boolean function is a function whose arguments, as well as the function itself, assume values from a two-element set. Alternative names are switching function, used especially in older computer science literature, and truth function, used in logic. Boolean functions are the subject of Boolean algebra and switching theory.
System F, also known as the (Girard–Reynolds) polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types. System F thus formalizes the notion of parametric polymorphism in programming languages, and forms a theoretical basis for languages such as Haskell and ML. System F was discovered independently by logician Jean-Yves Girard (1972) and computer scientist John C. Reynolds (1974).
Bunched logic is a variety of substructural logic proposed by Peter O'Hearn and David Pym. Bunched logic provides primitives for reasoning about resource composition, which aid in the compositional analysis of computer and other systems. It has category-theoretic and truth-functional semantics which can be understood in terms of an abstract concept of resource, and a proof theory in which the contexts Γ in an entailment judgement Γ ⊢ A are tree-like structures (bunches) rather than lists or (multi)sets as in most proof calculi. Bunched logic has an associated type theory, and its first application was in providing a way to control the aliasing and other forms of interference in imperative programs. The logic has seen further applications in program verification, where it is the basis of the assertion language of separation logic, and in systems modelling, where it provides a way to decompose the resources used by components of a system.
In computer science, a rough set, first described by Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set in terms of a pair of sets which give the lower and the upper approximation of the original set. In the standard version of rough set theory, the lower- and upper-approximation sets are crisp sets, but in other variations, the approximating sets may be fuzzy sets.

In probability theory and statistics, the probit function is the quantile function associated with the standard normal distribution. It has applications in data analysis and machine learning, in particular exploratory statistical graphics and specialized regression modeling of binary response variables.
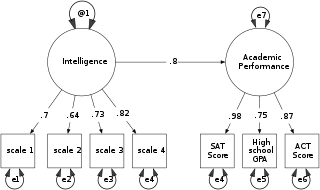
Structural equation modeling (SEM) is a label for a diverse set of methods used by scientists in both experimental and observational research across the sciences, business, and other fields. It is used most in the social and behavioral sciences. A definition of SEM is difficult without reference to highly technical language, but a good starting place is the name itself.
Richard Jay Lipton is an American-South African computer scientist who has worked in computer science theory, cryptography, and DNA computing. Lipton is Associate Dean of Research, Professor, and the Frederick G. Storey Chair in Computing in the College of Computing at the Georgia Institute of Technology.
In mathematical psychology, a knowledge space is a combinatorial structure describing the possible states of knowledge of a human learner. To form a knowledge space, one models a domain of knowledge as a set of concepts, and a feasible state of knowledge as a subset of that set containing the concepts known or knowable by some individual. Typically, not all subsets are feasible, due to prerequisite relations among the concepts. The knowledge space is the family of all the feasible subsets.
Group method of data handling (GMDH) is a family of inductive algorithms for computer-based mathematical modeling of multi-parametric datasets that features fully automatic structural and parametric optimization of models.
Boolean analysis was introduced by Flament (1976). The goal of a Boolean analysis is to detect deterministic dependencies between the items of a questionnaire or similar data-structures in observed response patterns. These deterministic dependencies have the form of logical formulas connecting the items. Assume, for example, that a questionnaire contains items i, j, and k. Examples of such deterministic dependencies are then i → j, i ∧ j → k, and i ∨ j → k.
In statistics, multiple correspondence analysis (MCA) is a data analysis technique for nominal categorical data, used to detect and represent underlying structures in a data set. It does this by representing data as points in a low-dimensional Euclidean space. The procedure thus appears to be the counterpart of principal component analysis for categorical data. MCA can be viewed as an extension of simple correspondence analysis (CA) in that it is applicable to a large set of categorical variables.
Quantum optimization algorithms are quantum algorithms that are used to solve optimization problems. Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. The power of quantum computing may allow problems which are not practically feasible on classical computers to be solved, or suggest a considerable speed up with respect to the best known classical algorithm.
Interpolation sort is a kind of bucket sort. It uses an interpolation formula to assign data to the bucket. A general interpolation formula is:











