In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.
In the mathematical area of knot theory, a Reidemeister move is any of three local moves on a link diagram. Kurt Reidemeister (1927) and, independently, James Waddell Alexander and Garland Baird Briggs (1926), demonstrated that two knot diagrams belonging to the same knot, up to planar isotopy, can be related by a sequence of the three Reidemeister moves.

Colin Conrad Adams is a mathematician primarily working in the areas of hyperbolic 3-manifolds and knot theory. His book, The Knot Book, has been praised for its accessible approach to advanced topics in knot theory. He is currently Francis Christopher Oakley Third Century Professor of Mathematics at Williams College, where he has been since 1985. He writes "Mathematically Bent", a column of math humor for the Mathematical Intelligencer.
In mathematics, the unknotting problem is the problem of algorithmically recognizing the unknot, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms. A major unresolved challenge is to determine if the problem admits a polynomial time algorithm; that is, whether the problem lies in the complexity class P.

Proceedings of the American Mathematical Society is a monthly peer-reviewed scientific journal of mathematics published by the American Mathematical Society. As a requirement, all articles must be at most 15 printed pages.

Louis Hirsch Kauffman is an American mathematician, topologist, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago. He is known for the introduction and development of the bracket polynomial and the Kauffman polynomial.
In knot theory, the self-linking number is an invariant of framed knots. It is related to the linking number of curves.

In the mathematical theory of knots, the stick number is a knot invariant that intuitively gives the smallest number of straight "sticks" stuck end to end needed to form a knot. Specifically, given any knot K, the stick number of K, denoted by stick(K), is the smallest number of edges of a polygonal path equivalent to K.
In the mathematical theory of knots, a Berge knot or doubly primitive knot is any member of a particular family of knots in the 3-sphere. A Berge knot K is defined by the conditions:
- K lies on a genus two Heegaard surface S
- in each handlebody bound by S, K meets some meridian disc exactly once.
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant. An invertible link is the link equivalent of an invertible knot.
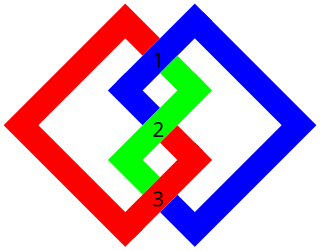
In the mathematical area of knot theory, the crossing number of a knot is the smallest number of crossings of any diagram of the knot. It is a knot invariant.

Sergei Gukov is a Russian-American mathematical and theoretical physicist. Gukov graduated from Moscow Institute of Physics and Technology (MIPT) in Moscow, Russia before obtaining a doctorate in physics from Princeton University under the supervision of Edward Witten.
The International Journal of Algebra and Computation is published by World Scientific, and contains articles on general mathematics, as well as:

The Journal of Nonlinear Mathematical Physics (JNMP) is a mathematical journal published by Atlantis Press. It covers nonlinear problems in physics and mathematics, include applications, with topics such as quantum algebras and integrability; non-commutative geometry; spectral theory; and instanton, monopoles and gauge theory.
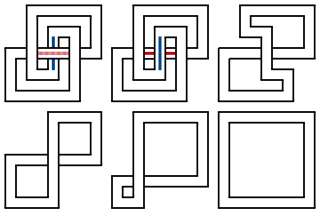
In the mathematical area of knot theory, the unknotting number of a knot is the minimum number of times the knot must be passed through itself to untie it. If a knot has unknotting number , then there exists a diagram of the knot which can be changed to unknot by switching crossings. The unknotting number of a knot is always less than half of its crossing number.
Order is a quarterly peer-reviewed academic journal on order theory and its applications, published by Springer Science+Business Media. It was established in 1984 by Ivan Rival. From 2010 to 2018, its editor-in-chief was Dwight Duffus. He was succeeded in 2019 by Ryan R. Martin.

The Journal of Group Theory is a bimonthly peer-reviewed mathematical journal covering all aspects of group theory. It was established in 1998 and is published by Walter de Gruyter. The editor-in-chief is Chris Parker.

Discrete Applied Mathematics is a peer-reviewed scientific journal covering algorithmic and applied areas of discrete mathematics. It is published by Elsevier and the editor-in-chief is Endre Boros. The journal was split off from another Elsevier journal, Discrete Mathematics, in 1979, with that journal's founder Peter Ladislaw Hammer as its founding editor-in-chief.

Combinatorics, Probability and Computing is a peer-reviewed scientific journal in mathematics published by Cambridge University Press. Its editor-in-chief is Béla Bollobás. The journal covers combinatorics, probability theory, and theoretical computer science. Currently, it publishes six issues annually. As with other journals from the same publisher, it follows a hybrid green/gold open access policy, in which authors may either place copies of their papers in an institutional repository after a six-month embargo period, or pay an open access charge to make their papers free to read on the journal's website.
Hernando Burgos Soto is a Canadian writer and mathematician, professor of mathematics at George Brown College. He is the author of several math papers in which he introduced some mathematics concepts and extended to tangles some celebrated results of knot theory about the Khovanov homology and the Jones polynomial. During his career as a mathematician, his interests have included Mathematical Statistics, Knot Theory, Algebraic Topology and more recently Mathematical Finance. He is comfortable writing in English and Spanish. When writing in Spanish, he works in the area of prose fiction writing short stories. Some of his short stories were published at the website Cuentos y Cuentos.