In geometric topology, a branch of mathematics, the lantern relation is a relation that appears between certain Dehn twists in the mapping class group of a surface. The most general version of the relation involves seven Dehn twists. The relation was discovered by Dennis Johnson in 1979. [1]
The general form of the lantern relation involves seven Dehn twists in the mapping class group of a disk with three holes, [1] [2] as shown in the figure on the right. According to the relation,
where DA, DB, and DC are the right-handed Dehn twists around the blue curves A, B, and C, and DR, DS, DT, DU are the right-handed Dehn twists around the four red curves.
Note that the Dehn twists DR, DS, DT, DU on the right-hand side all commute (since the curves are disjoint, so the order in which they appear does not matter. However, the cyclic order of the three Dehn twists on the left does matter:
Also, note that the equalities written above are actually equality up to homotopy or isotopy, as is usual in the mapping class group.
Though we have stated the lantern relation for a disk with three holes, the relation appears in the mapping class group of any surface in which such a disk can be embedded in a nontrivial way. Depending on the setting, some of the Dehn twists appearing in the lantern relation may be homotopic to the identity function, in which case the relation involves fewer than seven Dehn twists.
The lantern relation is used in several different presentations for the mapping class groups of surfaces.
In mathematics, a diffeomorphism is an isomorphism of smooth manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are differentiable.
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. The word homeomorphism comes from the Greek words ὅμοιος (homoios) = similar or same and μορφή (morphē) = shape or form, introduced to mathematics by Henri Poincaré in 1895.
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.
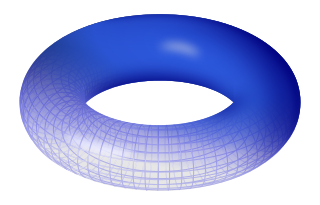
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.
Max Wilhelm Dehn was a German mathematician most famous for his work in geometry, topology and geometric group theory. Born to a Jewish family in Germany, Dehn's early life and career took place in Germany. However, he was forced to retire in 1935 and eventually fled Germany in 1939 and emigrated to the United States.
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.
In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface.
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting about their precise geometry. Unlike homology groups, which are also topological invariants, the homotopy groups are surprisingly complex and difficult to compute.
In topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link. It is often conceptualized as two steps: drilling then filling.
In mathematics, the Teichmüller space of a (real) topological surface , is a space that parametrizes complex structures on up to the action of homeomorphisms that are isotopic to the identity homeomorphism. Teichmüller spaces are named after Oswald Teichmüller.
In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.1416.
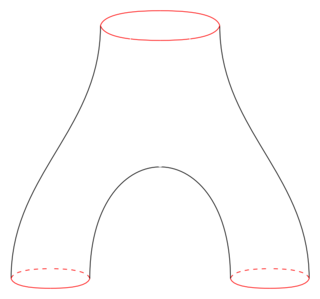
In mathematics, a pair of pants is a surface which is homeomorphic to the three-holed sphere. The name comes from considering one of the removed disks as the waist and the two others as the cuffs of a pair of pants.
In the mathematical subject of geometric group theory, a Dehn function, named after Max Dehn, is an optimal function associated to a finite group presentation which bounds the area of a relation in that group in terms of the length of that relation. The growth type of the Dehn function is a quasi-isometry invariant of a finitely presented group. The Dehn function of a finitely presented group is also closely connected with non-deterministic algorithmic complexity of the word problem in groups. In particular, a finitely presented group has solvable word problem if and only if the Dehn function for a finite presentation of this group is recursive. The notion of a Dehn function is motivated by isoperimetric problems in geometry, such as the classic isoperimetric inequality for the Euclidean plane and, more generally, the notion of a filling area function that estimates the area of a minimal surface in a Riemannian manifold in terms of the length of the boundary curve of that surface.
In mathematics, and more precisely in topology, the mapping class group of a surface, sometimes called the modular group or Teichmüller modular group, is the group of homeomorphisms of the surface viewed up to continuous deformation. It is of fundamental importance for the study of 3-manifolds via their embedded surfaces and is also studied in algebraic geometry in relation to moduli problems for curves.
Introduction to 3-Manifolds is a mathematics book on low-dimensional topology. It was written by Jennifer Schultens and published by the American Mathematical Society in 2014 as volume 151 of their book series Graduate Studies in Mathematics.
Braids, Links, and Mapping Class Groups is a mathematical monograph on braid groups and their applications in low-dimensional topology. It was written by Joan Birman, based on lecture notes by James W. Cannon, and published in 1974 by the Princeton University Press and University of Tokyo Press, as volume 82 of the book series Annals of Mathematics Studies.
 | This topology-related article is a stub. You can help Wikipedia by expanding it. |