Levenshtein automaton

Last updated

In computer science, a Levenshtein automaton for a string w and a number n is a finite-state automaton that can recognize the set of all strings whose Levenshtein distance from w is at most n. That is, a string x is in the formal language recognized by the Levenshtein automaton if and only if x can be transformed into w by at most n single-character insertions, deletions, and substitutions. [1]

Contents

Applications

Levenshtein automata may be used for spelling correction, by finding words in a given dictionary that are close to a misspelled word. In this application, once a word is identified as being misspelled, its Levenshtein automaton may be constructed, and then applied to all of the words in the dictionary to determine which ones are close to the misspelled word. If the dictionary is stored in compressed form as a trie, the time for this algorithm (after the automaton has been constructed) is proportional to the number of nodes in the trie, significantly faster than using dynamic programming to compute the Levenshtein distance separately for each dictionary word. [1]

It is also possible to find words in a regular language, rather than a finite dictionary, that are close to a given target word, by computing the Levenshtein automaton for the word, and then using a Cartesian product construction to combine it with an automaton for the regular language, giving an automaton for the intersection language. Alternatively, rather than using the product construction, both the Levenshtein automaton and the automaton for the given regular language may be traversed simultaneously using a backtracking algorithm. [1]

Levenshtein automata are used in Lucene for full-text searches that can return relevant documents even if the query is misspelled. [2]

Construction

For any fixed constant n, the Levenshtein automaton for w and n may be constructed in time O(|w|). [1]

Mitankin studies a variant of this construction called the universal Levenshtein automaton, determined only by a numeric parameter n, that can recognize pairs of words (encoded in a certain way by bitvectors) that are within Levenshtein distance n of each other. [3] Touzet proposed an effective algorithm to build this automaton. [4]

Yet a third finite automaton construction of Levenshtein (or Damerau–Levenshtein) distance are the Levenshtein transducers of Hassan et al., who show finite state transducers implementing edit distance one, then compose these to implement edit distances up to some constant. [5]

See also

Related Research Articles

<span class="mw-page-title-main">Finite-state machine</span> Mathematical model of computation

A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.

In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.

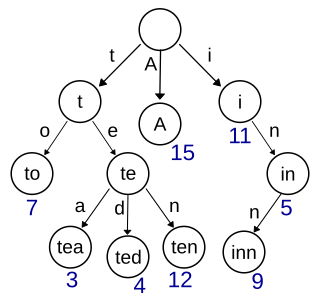
<span class="mw-page-title-main">Trie</span> K-ary search tree data structure

In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.

<span class="mw-page-title-main">Automata theory</span> Study of abstract machines and automata

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.

In information theory, linguistics, and computer science, the Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two words is the minimum number of single-character edits required to change one word into the other. It is named after the Soviet mathematician Vladimir Levenshtein, who considered this distance in 1965.

In computational linguistics and computer science, edit distance is a string metric, i.e. a way of quantifying how dissimilar two strings are to one another, that is measured by counting the minimum number of operations required to transform one string into the other. Edit distances find applications in natural language processing, where automatic spelling correction can determine candidate corrections for a misspelled word by selecting words from a dictionary that have a low distance to the word in question. In bioinformatics, it can be used to quantify the similarity of DNA sequences, which can be viewed as strings of the letters A, C, G and T.

<span class="mw-page-title-main">Deterministic finite automaton</span> Finite-state machine

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.

In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if

A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines relations between sets of strings.

The ω-regular languages are a class of ω-languages that generalize the definition of regular languages to infinite words.

In information theory and computer science, the Damerau–Levenshtein distance is a string metric for measuring the edit distance between two sequences. Informally, the Damerau–Levenshtein distance between two words is the minimum number of operations required to change one word into the other.

In formal language theory, an alphabet, sometimes called a vocabulary, is a non-empty set of indivisible symbols/glyphs, typically thought of as representing letters, characters, digits, phonemes, or even words. Alphabets in this technical sense of a set are used in a diverse range of fields including logic, mathematics, computer science, and linguistics. An alphabet may have any cardinality ("size") and depending on its purpose maybe be finite, countable, or even uncountable.

<span class="mw-page-title-main">Deterministic acyclic finite state automaton</span>

In computer science, a deterministic acyclic finite state automaton (DAFSA), also called a directed acyclic word graph is a data structure that represents a set of strings, and allows for a query operation that tests whether a given string belongs to the set in time proportional to its length. Algorithms exist to construct and maintain such automata, while keeping them minimal.

<span class="mw-page-title-main">DFA minimization</span>

In automata theory, DFA minimization is the task of transforming a given deterministic finite automaton (DFA) into an equivalent DFA that has a minimum number of states. Here, two DFAs are called equivalent if they recognize the same regular language. Several different algorithms accomplishing this task are known and described in standard textbooks on automata theory.

In computer science, Thompson's construction algorithm, also called the McNaughton–Yamada–Thompson algorithm, is a method of transforming a regular expression into an equivalent nondeterministic finite automaton (NFA). This NFA can be used to match strings against the regular expression. This algorithm is credited to Ken Thompson.

In computational learning theory, induction of regular languages refers to the task of learning a formal description of a regular language from a given set of example strings. Although E. Mark Gold has shown that not every regular language can be learned this way, approaches have been investigated for a variety of subclasses. They are sketched in this article. For learning of more general grammars, see Grammar induction.

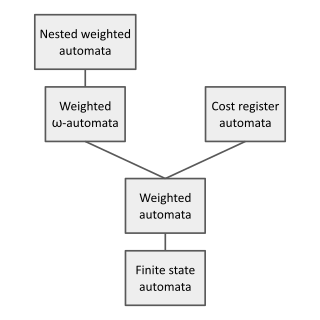
<span class="mw-page-title-main">Weighted automaton</span> Finite-state machine where edges carry weights

In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.

<span class="mw-page-title-main">Suffix automaton</span> Deterministic finite automaton accepting set of all suffixes of particular string

In computer science, a suffix automaton is an efficient data structure for representing the substring index of a given string which allows the storage, processing, and retrieval of compressed information about all its substrings. The suffix automaton of a string is the smallest directed acyclic graph with a dedicated initial vertex and a set of "final" vertices, such that paths from the initial vertex to final vertices represent the suffixes of the string.

In automata theory, an unambiguous finite automaton (UFA) is a nondeterministic finite automaton (NFA) such that each word has at most one accepting path. Each deterministic finite automaton (DFA) is an UFA, but not vice versa. DFA, UFA, and NFA recognize exactly the same class of formal languages. On the one hand, an NFA can be exponentially smaller than an equivalent DFA. On the other hand, some problems are easily solved on DFAs and not on UFAs. For example, given an automaton A, an automaton A′ which accepts the complement of A can be computed in linear time when A is a DFA, it is not known whether it can be done in polynomial time for UFA. Hence UFAs are a mix of the worlds of DFA and of NFA; in some cases, they lead to smaller automata than DFA and quicker algorithms than NFA.

References

  1. 1 2 3 4 Schulz, Klaus U.; Mihov, Stoyan (2002). "Fast String Correction with Levenshtein-Automata" . International Journal of Document Analysis and Recognition. 5 (1): 67–85. CiteSeerX   10.1.1.16.652 . doi:10.1007/s10032-002-0082-8. S2CID   207046453.
  2. ↑ McCandless, Michael (24 March 2011). "Lucene's FuzzyQuery is 100 times faster in 4.0". Changing Bits. Retrieved 2021-06-07.
  3. ↑ Mitankin, Petar N. (2005). Universal Levenshtein Automata. Building and Properties (PDF) (Thesis). Sofia University St. Kliment Ohridski.
  4. ↑ Touzet H. (2016). "On the Levenshtein Automaton and the Size of the Neighbourhood of a Word" (PDF). Language and Automata Theory and Applications. Lecture Notes in Computer Science. Vol. 9618. Lecture Notes in Computer Science. pp. 207–218. doi:10.1007/978-3-319-30000-9_16. ISBN   978-3-319-29999-0. S2CID   34821290.
  5. ↑ Hassan, Ahmed; Noeman, Sara; Hassan, Hany (2008). Language Independent Text Correction using Finite State Automata. IJCNLP.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.