
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code proceeds by means of Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".

In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed. A string is generally considered as a data type and is often implemented as an array data structure of bytes that stores a sequence of elements, typically characters, using some character encoding. String may also denote more general arrays or other sequence data types and structures.
In computer science, string-searching algorithms, sometimes called string-matching algorithms, are an important class of string algorithms that try to find a place where one or several strings are found within a larger string or text.
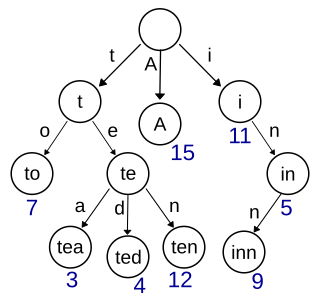
In computer science, a trie, also called digital tree or prefix tree, is a kind of search tree—an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated; i.e., the value of the key is distributed across the structure. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Keys tend to be associated with leaves, though some inner nodes may correspond to keys of interest. Hence, keys are not necessarily associated with every node. For the space-optimized presentation of prefix tree, see compact prefix tree.
In theoretical computer science, a Markov algorithm is a string rewriting system that uses grammar-like rules to operate on strings of symbols. Markov algorithms have been shown to be Turing-complete, which means that they are suitable as a general model of computation and can represent any mathematical expression from its simple notation. Markov algorithms are named after the Soviet mathematician Andrey Markov, Jr.
In computational linguistics and computer science, edit distance is a way of quantifying how dissimilar two strings are to one another by counting the minimum number of operations required to transform one string into the other. Edit distances find applications in natural language processing, where automatic spelling correction can determine candidate corrections for a misspelled word by selecting words from a dictionary that have a low distance to the word in question. In bioinformatics, it can be used to quantify the similarity of DNA sequences, which can be viewed as strings of the letters A, C, G and T.
In computer science, the Boyer–Moore string-search algorithm is an efficient string-searching algorithm that is the standard benchmark for practical string-search literature. It was developed by Robert S. Boyer and J Strother Moore in 1977. The original paper contained static tables for computing the pattern shifts without an explanation of how to produce them. The algorithm for producing the tables was published in a follow-on paper; this paper contained errors which were later corrected by Wojciech Rytter in 1980. The algorithm preprocesses the string being searched for, but not the string being searched in. It is thus well-suited for applications in which the pattern is much shorter than the text or where it persists across multiple searches. The Boyer–Moore algorithm uses information gathered during the preprocess step to skip sections of the text, resulting in a lower constant factor than many other string search algorithms. In general, the algorithm runs faster as the pattern length increases. The key features of the algorithm are to match on the tail of the pattern rather than the head, and to skip along the text in jumps of multiple characters rather than searching every single character in the text.

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full text indices, data compression algorithms, and the field of bibliometrics.

In computer science, a radix tree is a data structure that represents a space-optimized trie in which each node that is the only child is merged with its parent. The result is that the number of children of every internal node is at most the radix r of the radix tree, where r is a positive integer and a power x of 2, having x ≥ 1. Unlike regular trees, edges can be labeled with sequences of elements as well as single elements. This makes radix trees much more efficient for small sets and for sets of strings that share long prefixes.

In graph theory, an m-ary tree is a rooted tree in which each node has no more than m children. A binary tree is the special case where m = 2, and a ternary tree is another case with m = 3 that limits its children to three.
In computer science, the longest common substring problem is to find the longest string that is a substring of two or more strings. The problem may have multiple solutions. Applications include data deduplication and plagiarism detection.
In mathematics, in the areas of combinatorics and computer science, a Lyndon word is a nonempty string that is strictly smaller in lexicographic order than all of its rotations. Lyndon words are named after mathematician Roger Lyndon, who investigated them in 1954, calling them standard lexicographic sequences. Anatoly Shirshov introduced Lyndon words in 1953 calling them regular words. Lyndon words are a special case of Hall words; almost all properties of Lyndon words are shared by Hall words.
In computational phylogenetics, tree alignment is a computational problem concerned with producing multiple sequence alignments, or alignments of three or more sequences of DNA, RNA, or protein. Sequences are arranged into a phylogenetic tree, modeling the evolutionary relationships between species or taxa. The edit distances between sequences are calculated for each of the tree's internal vertices, such that the sum of all edit distances within the tree is minimized. Tree alignment can be accomplished using one of several algorithms with various trade-offs between manageable tree size and computational effort.
In formal language theory, a string is defined as a finite sequence of members of an underlying base set; this set is called the alphabet of a string or collection of strings. The members of the set are called symbols, and are typically thought of as representing letters, characters, or digits. For example, a common alphabet is {0,1}, the binary alphabet, and a binary string is a string drawn from the alphabet {0,1}. An infinite sequence of letters may be constructed from elements of an alphabet as well.
In computer science, a succinct data structure is a data structure which uses an amount of space that is "close" to the information-theoretic lower bound, but still allows for efficient query operations. The concept was originally introduced by Jacobson to encode bit vectors, (unlabeled) trees, and planar graphs. Unlike general lossless data compression algorithms, succinct data structures retain the ability to use them in-place, without decompressing them first. A related notion is that of a compressed data structure, in which the size of the data structure depends upon the particular data being represented.

The Wavelet Tree is a succinct data structure to store strings in compressed space. It generalizes the and operations defined on bitvectors to arbitrary alphabets.
In computer science, the longest common prefix array is an auxiliary data structure to the suffix array. It stores the lengths of the longest common prefixes (LCPs) between all pairs of consecutive suffixes in a sorted suffix array.
In the field of computational biology, a planted motif search (PMS) also known as a (l, d)-motif search (LDMS) is a method for identifying conserved motifs within a set of nucleic acid or peptide sequences.
The Garsia–Wachs algorithm is an efficient method for computers to construct optimal binary search trees and alphabetic Huffman codes, in linearithmic time. It is named after Adriano Garsia and Michelle L. Wachs.














