Ternary search tree

Last updated
Ternary Search Tree (TST)
Type tree
Time complexity in big O notation
OperationAverageWorst case
Search O(log n) O(n)
Insert O(log n) O(n)
Delete O(log n) O(n)
Space complexity

In computer science, a ternary search tree is a type of trie (sometimes called a prefix tree) where nodes are arranged in a manner similar to a binary search tree, but with up to three children rather than the binary tree's limit of two. Like other prefix trees, a ternary search tree can be used as an associative map structure with the ability for incremental string search. However, ternary search trees are more space efficient compared to standard prefix trees, at the cost of speed. Common applications for ternary search trees include spell-checking and auto-completion.

Contents

Description

Each node of a ternary search tree stores a single character, an object (or a pointer to an object depending on implementation), and pointers to its three children conventionally named equal kid, lo kid and hi kid, which can also be referred respectively as middle (child), lower (child) and higher (child). [1] A node may also have a pointer to its parent node as well as an indicator as to whether or not the node marks the end of a word. [2] The lo kid pointer must point to a node whose character value is less than the current node. The hi kid pointer must point to a node whose character is greater than the current node. [1] The equal kid points to the next character in the word. The figure below shows a ternary search tree with the strings "cute","cup","at","as","he","us" and "i":

          c         / | \        a  u  h        |  |  | \        t  t  e  u      /  / |   / |     s  p  e  i  s

As with other trie data structures, each node in a ternary search tree represents a prefix of the stored strings. All strings in the middle subtree of a node start with that prefix.

Operations

Insertion

Inserting a value into a ternary search can be defined recursively or iteratively much as lookups are defined. This recursive method is continually called on nodes of the tree given a key which gets progressively shorter by pruning characters off the front of the key. If this method reaches a node that has not been created, it creates the node and assigns it the character value of the first character in the key. Whether a new node is created or not, the method checks to see if the first character in the string is greater than or less than the character value in the node and makes a recursive call on the appropriate node as in the lookup operation. If, however, the key's first character is equal to the node's value then the insertion procedure is called on the equal kid and the key's first character is pruned away. [1] Like binary search trees and other data structures, ternary search trees can become degenerate depending on the order of the keys. [3] [ self-published source? ] Inserting keys in alphabetical order is one way to attain the worst possible degenerate tree. [1] Inserting the keys in random order often produces a well-balanced tree. [1] 

functioninsertion(stringkey)isnodep:=root//initialized to be equal in case root is nullnodelast:=rootintidx:=0whilepisnotnulldo//recurse on proper subtreeifkey[idx]<p.splitcharthenlast:=pp:=p.leftelseifkey[idx]>p.splitcharthenlast:=pp:=p.rightelse:// key is already in our Treeifidx==length(key)thenreturn//trim character from our key idx:=idx+1last:=pp:=p.midp:=node()//add p in as a child of the last non-null node (or root if root is null)ifroot==nullthenroot:=pelseiflast.splitchar<key[idx]thenlast.right:=pelseiflast.splitchar>key[idx]thenlast.left:=pelselast.mid:=pp.splitchar:=key[idx]idx:=idx+1// Insert remainder of keywhileidx<length(key)dop.mid:=node()p.mid.splitchar:=key[idx]idx+=1

To look up a particular node or the data associated with a node, a string key is needed. A lookup procedure begins by checking the root node of the tree and determining which of the following conditions has occurred. If the first character of the string is less than the character in the root node, a recursive lookup can be called on the tree whose root is the lo kid of the current root. Similarly, if the first character is greater than the current node in the tree, then a recursive call can be made to the tree whose root is the hi kid of the current node. [1] As a final case, if the first character of the string is equal to the character of the current node then the function returns the node if there are no more characters in the key. If there are more characters in the key then the first character of the key must be removed and a recursive call is made given the equal kid node and the modified key. [1] This can also be written in a non-recursive way by using a pointer to the current node and a pointer to the current character of the key. [1]

Pseudocode

functionsearch(stringquery)isifis_empty(query)thenreturnfalsenodep:=rootintidx:=0whilepisnotnulldoifquery[idx]<p.splitcharthenp:=p.leftelseifquery[idx]>p.splitcharthenp:=p.right;elseifidx=length(query)thenreturntrueidx:=idx+1p:=p.midreturnfalse

Deletion

The delete operation consists of searching for a key string in the search tree and finding a node, called firstMid in the below pseudocode, such that the path from the middle child of firstMid to the end of the search path for the key string has no left or right children. This would represent a unique suffix in the ternary tree corresponding to the key string. If there is no such path, this means that the key string is either fully contained as a prefix of another string, or is not in the search tree. Many implementations make use of an end of string character to ensure only the latter case occurs. The path is then deleted from firstMid.mid to the end of the search path. In the case that firstMid is the root, the key string must have been the last string in the tree, and thus the root is set to null after the deletion. 

functiondelete(stringkey)isifis_empty(key)thenreturnnodep:=rootintidx:=0nodefirstMid:=nullwhilepisnotnulldoifkey[idx]<p.splitcharthenfirstMid:=nullp:=p.leftelseifkey[idx]>p.splitcharthenfirstMid:=nullp:=p.rightelsefirstMid:=pwhilepisnotnullandkey[idx]==p.splitchardoidx:=idx+1p:=p.midiffirstMid==nullthenreturn// No unique string suffix// At this point, firstMid points to the node before the strings unique suffix occursnodeq:=firstMid.midnodep:=qfirstMid.mid:=null// disconnect suffix from treewhileqisnotnulldo//walk down suffix path and delete nodes p:=qq:=q.middelete(p)// free memory associated with node piffirstMid==rootthendelete(root)//delete the entire treeroot:=null

Traversal

[ clarification needed ][ example needed ]

Partial-match searching

[ clarification needed ][ example needed ]

Near-neighbor searching

[ clarification needed ][ example needed ]

Running time

The running time of ternary search trees varies significantly with the input. Ternary search trees run best when given several similar strings, especially when those strings share a common prefix. Alternatively, ternary search trees are effective when storing a large number of relatively short strings (such as words in a dictionary). [1] Running times for ternary search trees are similar to binary search trees, in that they typically run in logarithmic time, but can run in linear time in the degenerate (worst) case. Further, the size of the strings must also be kept in mind when considering runtime. For example, in the search path for a string of length k, there will be k traversals down middle children in the tree, as well as a logarithmic number of traversals down left and right children in the tree. Thus, in a ternary search tree on a small number of very large strings the lengths of the strings can dominate the runtime. [4]

Time complexities for ternary search tree operations: [1]

Average-case running timeWorst-case running time
LookupO(log n + k)O(n + k)
InsertionO(log n + k)O(n + k)
DeleteO(log n + k)O(n + k)

Comparison to other data structures

Tries

While being slower than other prefix trees, ternary search trees can be better suited for larger data sets due to their space-efficiency. [1]

Hash maps

Hashtables can also be used in place of ternary search trees for mapping strings to values. However, hash maps also frequently use more memory than ternary search trees (but not as much as tries). Additionally, hash maps are typically slower at reporting a string that is not in the same data structure, because it must compare the entire string rather than just the first few characters. There is some evidence that shows ternary search trees running faster than hash maps. [1] Additionally, hash maps do not allow for many of the uses of ternary search trees, such as near-neighbor lookups.

DAFSAs (deterministic acyclic finite state automaton)

If storing dictionary words is all that is required (i.e., storage of information auxiliary to each word is not required), a minimal deterministic acyclic finite state automaton (DAFSA) would use less space than a trie or a ternary search tree. This is because a DAFSA can compress identical branches from the trie which correspond to the same suffixes (or parts) of different words being stored.

Uses

Ternary search trees can be used to solve many problems in which a large number of strings must be stored and retrieved in an arbitrary order. Some of the most common or most useful of these are below:

See also

Related Research Articles

<span class="mw-page-title-main">Binary search tree</span> Rooted binary tree data structure

In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is linear with respect to the height of the tree.

In computer science, a red–black tree is a self-balancing binary search tree data structure noted for fast storage and retrieval of ordered information. The nodes in a red-black tree hold an extra "color" bit, often drawn as red and black, which help ensure that the tree is always approximately balanced.

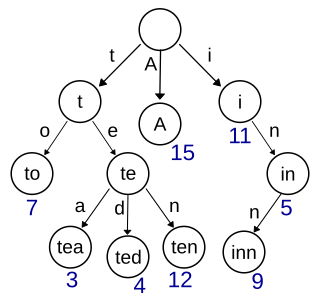
<span class="mw-page-title-main">Trie</span> Search tree data structure

In computer science, a trie, also called digital tree or prefix tree, is a type of search tree: specifically, a k-ary tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.

<span class="mw-page-title-main">Aho–Corasick algorithm</span> String-searching algorithm

In computer science, the Aho–Corasick algorithm is a string-searching algorithm invented by Alfred V. Aho and Margaret J. Corasick in 1975. It is a kind of dictionary-matching algorithm that locates elements of a finite set of strings within an input text. It matches all strings simultaneously. The complexity of the algorithm is linear in the length of the strings plus the length of the searched text plus the number of output matches. Note that because all matches are found, multiple matches will be returned for one string location if multiple substrings matched.

In computer science, tree traversal is a form of graph traversal and refers to the process of visiting each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.

<span class="mw-page-title-main">Suffix tree</span> Tree containing all suffixes of a given text

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.

In computer science, a search tree is a tree data structure used for locating specific keys from within a set. In order for a tree to function as a search tree, the key for each node must be greater than any keys in subtrees on the left, and less than any keys in subtrees on the right.

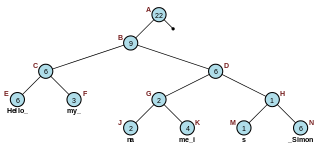
<span class="mw-page-title-main">Rope (data structure)</span> Data structure for storing strings

In computer programming, a rope, or cord, is a data structure composed of smaller strings that is used to efficiently store and manipulate longer strings or entire texts. For example, a text editing program may use a rope to represent the text being edited, so that operations such as insertion, deletion, and random access can be done efficiently.

<span class="mw-page-title-main">Radix tree</span> Data structure

In computer science, a radix tree is a data structure that represents a space-optimized trie in which each node that is the only child is merged with its parent. The result is that the number of children of every internal node is at most the radix r of the radix tree, where r = 2x for some integer x ≥ 1. Unlike regular trees, edges can be labeled with sequences of elements as well as single elements. This makes radix trees much more efficient for small sets and for sets of strings that share long prefixes.

In computer programming, a sentinel node is a specifically designated node used with linked lists and trees as a traversal path terminator. This type of node does not hold or reference any data managed by the data structure.

<span class="mw-page-title-main">Recursion (computer science)</span> Use of functions that call themselves

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.

The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.

<span class="mw-page-title-main">Ternary tree</span>

In computer science, a ternary tree is a tree data structure in which each node has at most three child nodes, usually distinguished as "left", “mid” and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to the "root" node, if it exists. Any node in the data structure can be reached by starting at root node and repeatedly following references to either the left, mid or right child.

In computer science, an x-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O(log log M), using O(n log M) space, where n is the number of stored values and M is the maximum value in the domain. The structure was proposed by Dan Willard in 1982, along with the more complicated y-fast trie, as a way to improve the space usage of van Emde Boas trees, while retaining the O(log log M) query time.

A concurrent hash-trie or Ctrie is a concurrent thread-safe lock-free implementation of a hash array mapped trie. It is used to implement the concurrent map abstraction. It has particularly scalable concurrent insert and remove operations and is memory-efficient. It is the first known concurrent data-structure that supports O(1), atomic, lock-free snapshots.

<span class="mw-page-title-main">ParaSail (programming language)</span>

Parallel Specification and Implementation Language (ParaSail) is an object-oriented parallel programming language. Its design and ongoing implementation is described in a blog and on its official website.

The HAT-trie is a type of radix trie that uses array nodes to collect individual key–value pairs under radix nodes and hash buckets into an associative array. Unlike a simple hash table, HAT-tries store key–value in an ordered collection. The original inventors are Nikolas Askitis and Ranjan Sinha. Askitis & Zobel showed that building and accessing the HAT-trie key/value collection is considerably faster than other sorted access methods and is comparable to the array hash which is an unsorted collection. This is due to the cache-friendly nature of the data structure which attempts to group access to data in time and space into the 64 byte cache line size of the modern CPU.

Multi-key quicksort, also known as three-way radix quicksort, is an algorithm for sorting strings. This hybrid of quicksort and radix sort was originally suggested by P. Shackleton, as reported in one of C.A.R. Hoare's seminal papers on quicksort; its modern incarnation was developed by Jon Bentley and Robert Sedgewick in the mid-1990s. The algorithm is designed to exploit the property that in many problems, strings tend to have shared prefixes.

A bitwise trie is a special form of trie where each node with its child-branches represents a bit sequence of one or more bits of a key. A bitwise trie with bitmap uses a bitmap to denote valid child branches.

References

  1. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 "Ternary Search Trees". Dr. Dobb's .
  2. 1 2 Ostrovsky, Igor. "Efficient auto-complete with a ternary search tree".
  3. 1 2 Wrobel, Lukasz. "Ternary Search Tree".
  4. ↑ Bentley, Jon; Sedgewick, Bob. "Ternary Search Tree".
  5. 1 2 3 Flint, Wally (February 16, 2001). "Plant your data in a ternary search tree". JavaWorld . Retrieved 2020-07-19.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.