In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed. A string is generally considered as a data type and is often implemented as an array data structure of bytes that stores a sequence of elements, typically characters, using some character encoding. String may also denote more general arrays or other sequence data types and structures.

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example,

In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.

Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. Extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored.

In the mathematical disciplines of topology and geometry, an orbifold is a generalization of a manifold. Roughly speaking, an orbifold is a topological space which is locally a finite group quotient of a Euclidean space.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full-text indices, data-compression algorithms, and the field of bibliometrics.

In graph theory and network analysis, indicators of centrality assign numbers or rankings to nodes within a graph corresponding to their network position. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, super-spreaders of disease, and brain networks. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.
In computer science, a longest common substring of two or more strings is a longest string that is a substring of all of them. There may be more than one longest common substring. Applications include data deduplication and plagiarism detection.
In computational phylogenetics, tree alignment is a computational problem concerned with producing multiple sequence alignments, or alignments of three or more sequences of DNA, RNA, or protein. Sequences are arranged into a phylogenetic tree, modeling the evolutionary relationships between species or taxa. The edit distances between sequences are calculated for each of the tree's internal vertices, such that the sum of all edit distances within the tree is minimized. Tree alignment can be accomplished using one of several algorithms with various trade-offs between manageable tree size and computational effort.
In computer science, a kernelization is a technique for designing efficient algorithms that achieve their efficiency by a preprocessing stage in which inputs to the algorithm are replaced by a smaller input, called a "kernel". The result of solving the problem on the kernel should either be the same as on the original input, or it should be easy to transform the output on the kernel to the desired output for the original problem.
In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.

A top tree is a data structure based on a binary tree for unrooted dynamic trees that is used mainly for various path-related operations. It allows simple divide-and-conquer algorithms. It has since been augmented to maintain dynamically various properties of a tree such as diameter, center and median.
In computer science, the longest palindromic substring or longest symmetric factor problem is the problem of finding a maximum-length contiguous substring of a given string that is also a palindrome. For example, the longest palindromic substring of "bananas" is "anana". The longest palindromic substring is not guaranteed to be unique; for example, in the string "abracadabra", there is no palindromic substring with length greater than three, but there are two palindromic substrings with length three, namely, "aca" and "ada". In some applications it may be necessary to return all maximal palindromic substrings rather than returning only one substring or returning the maximum length of a palindromic substring.

The Wavelet Tree is a succinct data structure to store strings in compressed space. It generalizes the and operations defined on bitvectors to arbitrary alphabets.
In computer science, the longest common prefix array is an auxiliary data structure to the suffix array. It stores the lengths of the longest common prefixes (LCPs) between all pairs of consecutive suffixes in a sorted suffix array.

In computer science, a suffix automaton is an efficient data structure for representing the substring index of a given string which allows the storage, processing, and retrieval of compressed information about all its substrings. The suffix automaton of a string is the smallest directed acyclic graph with a dedicated initial vertex and a set of "final" vertices, such that paths from the initial vertex to final vertices represent the suffixes of the string.

In graph theory, the Graham–Pollak theorem states that the edges of an -vertex complete graph cannot be partitioned into fewer than complete bipartite graphs. It was first published by Ronald Graham and Henry O. Pollak in two papers in 1971 and 1972, in connection with an application to telephone switching circuitry.
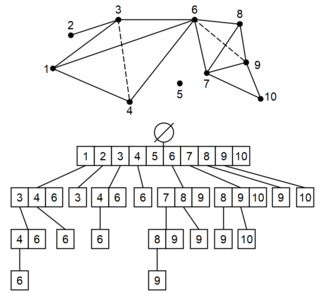
In topological data analysis, a simplex tree is a type of trie used to represent efficiently any general simplicial complex. Through its nodes, this data structure notably explicitly represents all the simplices. Its flexible structure allows implementation of many basic operations useful to computing persistent homology. This data structure was invented by Jean-Daniel Boissonnat and Clément Maria in 2014, in the article The Simplex Tree: An Efficient Data Structure for General Simplicial Complexes. This data structure offers efficient operations on sparse simplicial complexes. For dense or maximal simplices, Skeleton-Blocker representations or Toplex Map representations are used.
























