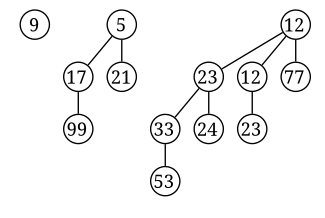
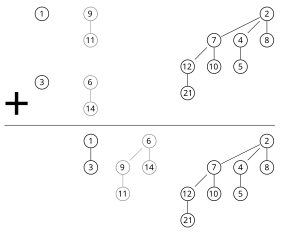
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is linear with respect to the height of the tree.

In computer science, a heap is a tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.
In computer science, a priority queue is an abstract data-type similar to a regular queue or stack data structure. Each element in a priority queue has an associated priority. In a priority queue, elements with high priority are served before elements with low priority. In some implementations, if two elements have the same priority, they are served in the same order in which they were enqueued. In other implementations, the order of elements with the same priority is undefined.

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.
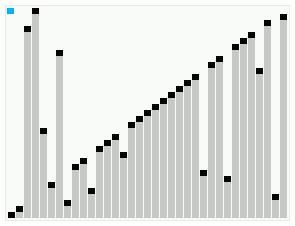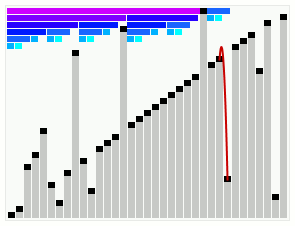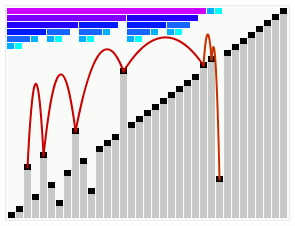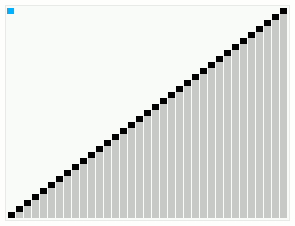
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n) operations (see big O notation), but it is not a stable sort. The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.
In computer science, a Fibonacci heap is a data structure for priority queue operations, consisting of a collection of heap-ordered trees. Fibonacci heaps were originally explained to be an extension of binomial queues. It has a better amortized running time than many other priority queue data structures including the binary heap and binomial heap. Michael L. Fredman and Robert E. Tarjan developed Fibonacci heaps in 1984 and published them in a scientific journal in 1987. Fibonacci heaps are named after the Fibonacci numbers, which are used in their running time analysis.
In computer science, a 2–3 heap is a data structure, a variation on the heap, designed by Tadao Takaoka in 1999. The structure is similar to the Fibonacci heap, and borrows from the 2–3 tree.
In computer science, a leftist tree or leftist heap is a priority queue implemented with a variant of a binary heap. Every node x has an s-value which is the distance to the nearest leaf in subtree rooted at x. In contrast to a binary heap, a leftist tree attempts to be very unbalanced. In addition to the heap property, leftist trees are maintained so the right descendant of each node has the lower s-value.
A pairing heap is a type of heap data structure with relatively simple implementation and excellent practical amortized performance, introduced by Michael Fredman, Robert Sedgewick, Daniel Sleator, and Robert Tarjan in 1986. Pairing heaps are heap-ordered multiway tree structures, and can be considered simplified Fibonacci heaps. They are considered a "robust choice" for implementing such algorithms as Prim's MST algorithm, and support the following operations :
The d-ary heap or d-heap is a priority queue data structure, a generalization of the binary heap in which the nodes have d children instead of 2. Thus, a binary heap is a 2-heap, and a ternary heap is a 3-heap. According to Tarjan and Jensen et al., d-ary heaps were invented by Donald B. Johnson in 1975.
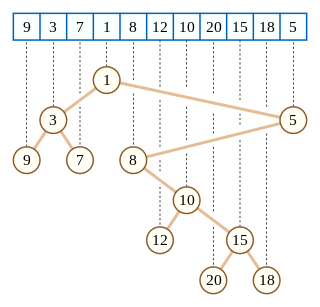
In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.
In computer science, a min-max heap is a complete binary tree data structure which combines the usefulness of both a min-heap and a max-heap, that is, it provides constant time retrieval and logarithmic time removal of both the minimum and maximum elements in it. This makes the min-max heap a very useful data structure to implement a double-ended priority queue. Like binary min-heaps and max-heaps, min-max heaps support logarithmic insertion and deletion and can be built in linear time. Min-max heaps are often represented implicitly in an array; hence it's referred to as an implicit data structure.
In computer science, a skew binomial heap is a variant of the binomial heap that supports constant-time insertion operations in the worst case, rather than the logarithmic worst case and constant amortized time of ordinary binomial heaps. Just as binomial heaps are based on the binary number system, skew binary heaps are based on the skew binary number system.
In computer science, the Brodal queue is a heap/priority queue structure with very low worst case time bounds: for insertion, find-minimum, meld and decrease-key and for delete-minimum and general deletion. They are the first heap variant to achieve these bounds without resorting to amortization of operational costs. Brodal queues are named after their inventor Gerth Stølting Brodal.
In computer science, k-way merge algorithms or multiway merges are a specific type of sequence merge algorithms that specialize in taking in k sorted lists and merging them into a single sorted list. These merge algorithms generally refer to merge algorithms that take in a number of sorted lists greater than two. Two-way merges are also referred to as binary merges.The k- way merge is also an external sorting algorithm.
In computer science, a weak heap is a data structure for priority queues, combining features of the binary heap and binomial heap. It can be stored in an array as an implicit binary tree like a binary heap, and has the efficiency guarantees of binomial heaps.
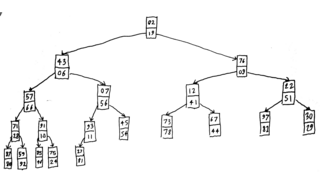
A K-D heap is a data structure in computer science which implements a multidimensional priority queue without requiring additional space. It is a generalization of the Heap. It allows for efficient insertion, query of the minimum element, and deletion of the minimum element in any of the k dimensions, and therefore includes the double-ended heap as a special case.
This is a comparison of the performance of notable data structures, as measured by the complexity of their logical operations. For a more comprehensive listing of data structures, see List of data structures.
In computer science, a strict Fibonacci heap is a priority queue data structure with worst case time bounds equal to the amortized bounds of the Fibonacci heap. Strict Fibonacci heaps belong to a class of asymptotically optimal data structures for priority queues. All operations on strict Fibonacci heaps run in worst case constant time except delete-min, which is necessarily logarithmic. This is optimal, because any priority queue can be used to sort a list of elements by performing insertions and delete-min operations. Strict Fibonacci heaps were invented in 2012 by Gerth Stølting Brodal, George Lagogiannis, and Robert E. Tarjan.