Double-ended priority queue

Last updated

In computer science, a double-ended priority queue (DEPQ) [1] or double-ended heap [2] is a data structure similar to a priority queue or heap, but allows for efficient removal of both the maximum and minimum, according to some ordering on the keys (items) stored in the structure. Every element in a DEPQ has a priority or value. In a DEPQ, it is possible to remove the elements in both ascending as well as descending order. [3]

Contents

Operations

UML class diagram of a double-ended priority queue. UML double-ended priortity queue.svg
UML class diagram of a double-ended priority queue.

A double-ended priority queue features the following operations:

isEmpty()
Checks if DEPQ is empty and returns true if empty.
size()
Returns the total number of elements present in the DEPQ.
getMin()
Returns the element having least priority.
getMax()
Returns the element having highest priority.
put(x)
Inserts the element x in the DEPQ.
removeMin()
Removes an element with minimum priority and returns this element.
removeMax()
Removes an element with maximum priority and returns this element.

Also, the priority of any element can be changed once it has been inserted in the DEPQ. [4]

Implementation

Double-ended priority queues can be built from balanced binary search trees (where the minimum and maximum elements are the leftmost and rightmost leaves, respectively), or using specialized data structures like min-max heap and pairing heap.

Generic methods of arriving at double-ended priority queues from normal priority queues are: [5]

Dual structure method

A dual structure with 14,12,4,10,8 as the members of DEPQ. Dual heap.jpg
A dual structure with 14,12,4,10,8 as the members of DEPQ.

In this method two different priority queues for min and max are maintained. The same elements in both the PQs are shown with the help of correspondence pointers.
Here, the minimum and maximum elements are values contained in the root nodes of min heap and max heap respectively.

Total correspondence

A total correspondence heap for the elements 3, 4, 5, 5, 6, 6, 7, 8, 9, 10, 11 with element 11 as buffer. Total correspondence heap.jpg
A total correspondence heap for the elements 3, 4, 5, 5, 6, 6, 7, 8, 9, 10, 11 with element 11 as buffer.

Half the elements are in the min PQ and the other half in the max PQ. Each element in the min PQ has a one-to-one correspondence with an element in max PQ. If the number of elements in the DEPQ is odd, one of the elements is retained in a buffer. [1] Priority of every element in the min PQ will be less than or equal to the corresponding element in the max PQ.

Leaf correspondence

A leaf correspondence heap for the same elements as above. Leaf correspondence.jpg
A leaf correspondence heap for the same elements as above.

In contrast to a total correspondence, in this method only the leaf elements of the min and max PQ form corresponding one-to-one pairs. It is not necessary for non-leaf elements to be in a one-to-one correspondence pair. [1] If the number of elements in the DEPQ is odd, one of the elements is retained in a buffer. [1]

Interval heaps

Implementing a DEPQ using interval heap. Interval heap depq.jpg
Implementing a DEPQ using interval heap.

Apart from the above-mentioned correspondence methods, DEPQ's can be obtained efficiently using interval heaps. [6] An interval heap is like an embedded min-max heap in which each node contains two elements. It is a complete binary tree in which: [6]

Depending on the number of elements, two cases are possible [6] -

  1. Even number of elements: In this case, each node contains two elements say p and q, with p ≤ q. Every node is then represented by the interval [p, q].
  2. Odd number of elements: In this case, each node except the last contains two elements represented by the interval [p, q] whereas the last node will contain a single element and is represented by the interval [p, p].

Inserting an element

Depending on the number of elements already present in the interval heap, following cases are possible:

  • Odd number of elements: If the number of elements in the interval heap is odd, the new element is firstly inserted in the last node. Then, it is successively compared with the previous node elements and tested to satisfy the criteria essential for an interval heap as stated above. In case if the element does not satisfy any of the criteria, it is moved from the last node to the root until all the conditions are satisfied. [6]
  • Even number of elements: If the number of elements is even, then for the insertion of a new element an additional node is created. If the element falls to the left of the parent interval, it is considered to be in the min heap and if the element falls to the right of the parent interval, it is considered in the max heap. Further, it is compared successively and moved from the last node to the root until all the conditions for interval heap are satisfied. If the element lies within the interval of the parent node itself, the process is stopped then and there itself and moving of elements does not take place. [6]

The time required for inserting an element depends on the number of movements required to meet all the conditions and is O(log n).

Deleting an element

  • Min element: In an interval heap, the minimum element is the element on the left hand side of the root node. This element is removed and returned. To fill in the vacancy created on the left hand side of the root node, an element from the last node is removed and reinserted into the root node. This element is then compared successively with all the left hand elements of the descending nodes and the process stops when all the conditions for an interval heap are satisfied. In case if the left hand side element in the node becomes greater than the right side element at any stage, the two elements are swapped [6] and then further comparisons are done. Finally, the root node will again contain the minimum element on the left hand side.
  • Max element: In an interval heap, the maximum element is the element on the right hand side of the root node. This element is removed and returned. To fill in the vacancy created on the right hand side of the root node, an element from the last node is removed and reinserted into the root node. Further comparisons are carried out on a similar basis as discussed above. Finally, the root node will again contain the max element on the right hand side.

Thus, with interval heaps, both the minimum and maximum elements can be removed efficiently traversing from root to leaf. Thus, a DEPQ can be obtained [6] from an interval heap where the elements of the interval heap are the priorities of elements in the DEPQ.

Time complexity

Interval heaps

When DEPQ's are implemented using Interval heaps consisting of n elements, the time complexities for the various functions are formulated in the table below [1]

OperationTime complexity
init()O(n)
isEmpty()O(1)
getmin()O(1)
getmax()O(1)
size()O(1)
insert(x)O(log n)
removeMin()O(log n)
removeMax()O(log n)

Pairing heaps

When DEPQ's are implemented using heaps or pairing heaps consisting of n elements, the time complexities for the various functions are formulated in the table below. [1] For pairing heaps, it is an amortized complexity.

OperationTime complexity
isEmpty()O(1)
getmin()O(1)
getmax()O(1)
insert(x)O(log n)
removeMax()O(log n)
removeMin()O(log n)

Applications

External sorting

One example application of the double-ended priority queue is external sorting. In an external sort, there are more elements than can be held in the computer's memory. The elements to be sorted are initially on a disk and the sorted sequence is to be left on the disk. The external quick sort is implemented using the DEPQ as follows:

  1. Read in as many elements as will fit into an internal DEPQ. The elements in the DEPQ will eventually be the middle group (pivot) of elements.
  2. Read in the remaining elements. If the next element is ≤ the smallest element in the DEPQ, output this next element as part of the left group. If the next element is ≥ the largest element in the DEPQ, output this next element as part of the right group. Otherwise, remove either the max or min element from the DEPQ (the choice may be made randomly or alternately); if the max element is removed, output it as part of the right group; otherwise, output the removed element as part of the left group; insert the newly input element into the DEPQ.
  3. Output the elements in the DEPQ, in sorted order, as the middle group.
  4. Sort the left and right groups recursively.

See also

Related Research Articles

<span class="mw-page-title-main">Heapsort</span> A sorting algorithm which uses the heap data structure

In computer science, heapsort is a comparison-based sorting algorithm which can be thought of as "an implementation of selection sort using the right data structure." Like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to efficiently find the largest element in each step.

<span class="mw-page-title-main">Heap (data structure)</span> Computer science data structure

In computer science, a heap is a tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.

In computer science, a priority queue is an abstract data type similar to a regular queue or stack abstract data type. Each element in a priority queue has an associated priority. In a priority queue, elements with high priority are served before elements with low priority. In some implementations, if two elements have the same priority, they are served in the same order in which they were enqueued. In other implementations, the order of elements with the same priority is undefined.

<span class="mw-page-title-main">Binary heap</span> Variant of heap data structure

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964 as a data structure for implementing heapsort.

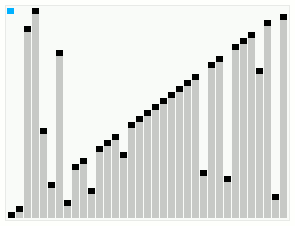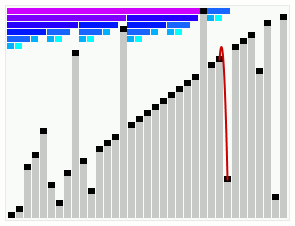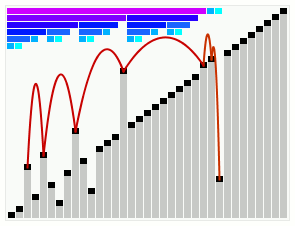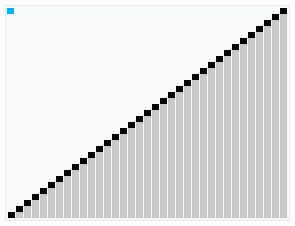
<span class="mw-page-title-main">Smoothsort</span> Comparison-based sorting algorithm

In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n) operations (see big O notation), but it is not a stable sort. The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.

<span class="mw-page-title-main">Treap</span> Random search tree data structure

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.

In computer science, a binomial heap is a data structure that acts as a priority queue. It is an example of a mergeable heap, as it supports merging two heaps in logarithmic time. It is implemented as a heap similar to a binary heap but using a special tree structure that is different from the complete binary trees used by binary heaps. Binomial heaps were invented in 1978 by Jean Vuillemin.

In computer science, a leftist tree or leftist heap is a priority queue implemented with a variant of a binary heap. Every node x has an s-value which is the distance to the nearest leaf in subtree rooted at x. In contrast to a binary heap, a leftist tree attempts to be very unbalanced. In addition to the heap property, leftist trees are maintained so the right descendant of each node has the lower s-value.

A pairing heap is a type of heap data structure with relatively simple implementation and excellent practical amortized performance, introduced by Michael Fredman, Robert Sedgewick, Daniel Sleator, and Robert Tarjan in 1986. Pairing heaps are heap-ordered multiway tree structures, and can be considered simplified Fibonacci heaps. They are considered a "robust choice" for implementing such algorithms as Prim's MST algorithm, and support the following operations :

The d-ary heap or d-heap is a priority queue data structure, a generalization of the binary heap in which the nodes have d children instead of 2. Thus, a binary heap is a 2-heap, and a ternary heap is a 3-heap. According to Tarjan and Jensen et al., d-ary heaps were invented by Donald B. Johnson in 1975.

<span class="mw-page-title-main">Cartesian tree</span> Binary tree derived from a sequence of numbers

In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.

In computer science, a search data structure is any data structure that allows the efficient retrieval of specific items from a set of items, such as a specific record from a database.

In computer science, a min-max heap is a complete binary tree data structure which combines the usefulness of both a min-heap and a max-heap, that is, it provides constant time retrieval and logarithmic time removal of both the minimum and maximum elements in it. This makes the min-max heap a very useful data structure to implement a double-ended priority queue. Like binary min-heaps and max-heaps, min-max heaps support logarithmic insertion and deletion and can be built in linear time. Min-max heaps are often represented implicitly in an array; hence it's referred to as an implicit data structure.

<span class="mw-page-title-main">Queap</span>

In computer science, a queap is a priority queue data structure. The data structure allows insertions and deletions of arbitrary elements, as well as retrieval of the highest-priority element. Each deletion takes amortized time logarithmic in the number of items that have been in the structure for a longer time than the removed item. Insertions take constant amortized time.

In computer science, a randomized meldable heap is a priority queue based data structure in which the underlying structure is also a heap-ordered binary tree. However, there are no restrictions on the shape of the underlying binary tree.

In computer science, k-way merge algorithms or multiway merges are a specific type of sequence merge algorithms that specialize in taking in k sorted lists and merging them into a single sorted list. These merge algorithms generally refer to merge algorithms that take in a number of sorted lists greater than two. Two-way merges are also referred to as binary merges. The k-way merge is also an external sorting algorithm.

In computer science, a weak heap is a data structure for priority queues, combining features of the binary heap and binomial heap. It can be stored in an array as an implicit binary tree like a binary heap, and has the efficiency guarantees of binomial heaps.

In computer science, a priority search tree is a tree data structure for storing points in two dimensions. It was originally introduced by Edward M. McCreight. It is effectively an extension of the priority queue with the purpose of improving the search time from O(n) to O(s + log n) time, where n is the number of points in the tree and s is the number of points returned by the search.

<span class="mw-page-title-main">K-D heap</span>

A K-D heap is a data structure in computer science which implements a multidimensional priority queue without requiring additional space. It is a generalization of the Heap. It allows for efficient insertion, query of the minimum element, and deletion of the minimum element in any of the k dimensions, and therefore includes the double-ended heap as a special case.

References

  1. 1 2 3 4 5 6 7 8 9 Data Structures, Algorithms, & Applications in Java: Double-Ended Priority Queues, Sartaj Sahni, 1999.
  2. ↑ Brass, Peter (2008). Advanced Data Structures. Cambridge University Press. p. 211. ISBN   9780521880374.
  3. ↑ "Depq - Double-Ended Priority Queue". Archived from the original on 2012-04-25. Retrieved 2011-10-04.
  4. ↑ "depq".
  5. ↑ Fundamentals of Data Structures in C++ - Ellis Horowitz, Sartaj Sahni and Dinesh Mehta
  6. 1 2 3 4 5 6 7 http://www.mhhe.com/engcs/compsci/sahni/enrich/c9/interval.pdf [ bare URL PDF ]
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.