Double-ended queue

"Deque" redirects here. Not to be confused with dequeueing, a queue operation.

Not to be confused with Double-ended priority queue.

In computer science, a double-ended queue (abbreviated to deque, pronounced deck, like "cheque" ^[1] ) is an abstract data type that generalizes a queue, for which elements can be added to or removed from either the front (head) or back (tail). ^[2] It is also often called a head-tail linked list, though properly this refers to a specific data structure implementation of a deque (see below).

Naming conventions

Deque is sometimes written dequeue, but this use is generally deprecated in technical literature or technical writing because dequeue is also a verb meaning "to remove from a queue". Nevertheless, several libraries and some writers, such as Aho, Hopcroft, and Ullman in their textbook Data Structures and Algorithms, spell it dequeue. John Mitchell, author of Concepts in Programming Languages, also uses this terminology.

Distinctions and sub-types

This differs from the queue abstract data type or first in first out list (FIFO), where elements can only be added to one end and removed from the other. This general data class has some possible sub-types:

• An input-restricted deque is one where deletion can be made from both ends, but insertion can be made at one end only.
• An output-restricted deque is one where insertion can be made at both ends, but deletion can be made from one end only.

Both the basic and most common list types in computing, queues and stacks can be considered specializations of deques, and can be implemented using deques.

Operations

UML class diagram of a double-ended queue

The basic operations on a deque are enqueue and dequeue on either end. Also generally implemented are peek operations, which return the value at that end without dequeuing it.

Names vary between languages; major implementations include:

operation	common name(s)	Ada	C++	Java	Perl	PHP	Python	Ruby	Rust	JavaScript
insert element at back	inject, snoc, push	Append	push_back	offerLast	push	array_push	append	push	push_back	push
insert element at front	push, cons	Prepend	push_front	offerFirst	unshift	array_unshift	appendleft	unshift	push_front	unshift
remove last element	eject	Delete_Last	pop_back	pollLast	pop	array_pop	pop	pop	pop_back	pop
remove first element	pop	Delete_First	pop_front	pollFirst	shift	array_shift	popleft	shift	pop_front	shift
examine last element	peek	Last_Element	back	peekLast	$array[-1]	end	<obj>[-1]	last	back	<obj>.at(-1)
examine first element		First_Element	front	peekFirst	$array[0]	reset	<obj>[0]	first	front	<obj>[0]

Implementations

There are at least two common ways to efficiently implement a deque: with a modified dynamic array or with a doubly linked list.

The dynamic array approach uses a variant of a dynamic array that can grow from both ends, sometimes called array deques. These array deques have all the properties of a dynamic array, such as constant-time random access, good locality of reference, and inefficient insertion/removal in the middle, with the addition of amortized constant-time insertion/removal at both ends, instead of just one end. Three common implementations include:

• Storing deque contents in a circular buffer, and only resizing when the buffer becomes full. This decreases the frequency of resizings.
• Allocating deque contents from the center of the underlying array, and resizing the underlying array when either end is reached. This approach may require more frequent resizings and waste more space, particularly when elements are only inserted at one end.
• Storing contents in multiple smaller arrays, allocating additional arrays at the beginning or end as needed. Indexing is implemented by keeping a dynamic array containing pointers to each of the smaller arrays.

Purely functional implementation

Double-ended queues can also be implemented as a purely functional data structure. ^{[3] : 115} Two versions of the implementation exist. The first one, called 'real-time deque, is presented below. It allows the queue to be persistent with operations in O(1) worst-case time, but requires lazy lists with memoization. The second one, with no lazy lists nor memoization is presented at the end of the sections. Its amortized time is O(1) if the persistency is not used; but the worst-time complexity of an operation is O(n) where n is the number of elements in the double-ended queue.

Let us recall that, for a list l, |l| denotes its length, that NIL represents an empty list and CONS(h, t) represents the list whose head is h and whose tail is t. The functions drop(i, l) and take(i, l) return the list l without its first i elements, and the first i elements of l, respectively. Or, if |l| < i, they return the empty list and l respectively.

Real-time deques via lazy rebuilding and scheduling

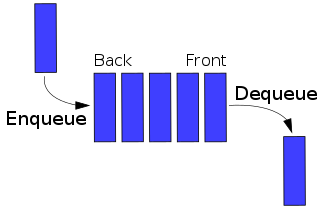
A double-ended queue is represented as a sextuple (len_front, front, tail_front, len_rear, rear, tail_rear) where front is a linked list which contains the front of the queue of length len_front. Similarly, rear is a linked list which represents the reverse of the rear of the queue, of length len_rear. Furthermore, it is assured that |front| ≤ 2|rear|+1 and |rear| ≤ 2|front|+1 - intuitively, it means that both the front and the rear contains between a third minus one and two thirds plus one of the elements. Finally, tail_front and tail_rear are tails of front and of rear, they allow scheduling the moment where some lazy operations are forced. Note that, when a double-ended queue contains n elements in the front list and n elements in the rear list, then the inequality invariant remains satisfied after i insertions and d deletions when (i+d) ≤ n/2. That is, at most n/2 operations can happen between each rebalancing.

Let us first give an implementation of the various operations that affect the front of the deque - cons, head and tail. Those implementations do not necessarily respect the invariant. In a second time we'll explain how to modify a deque which does not satisfy the invariant into one which satisfies it. However, they use the invariant, in that if the front is empty then the rear has at most one element. The operations affecting the rear of the list are defined similarly by symmetry.

empty=(0,NIL,NIL,0,NIL,NIL)funinsert'(x,(len_front,front,tail_front,len_rear,rear,tail_rear))=(len_front+1,CONS(x,front),drop(2,tail_front),len_rear,rear,drop(2,tail_rear))funhead((_,CONS(h,_),_,_,_,_))=hfunhead((_,NIL,_,_,CONS(h,NIL),_))=hfuntail'((len_front,CONS(head_front,front),tail_front,len_rear,rear,tail_rear))=(len_front-1,front,drop(2,tail_front),len_rear,rear,drop(2,tail_rear))funtail'((_,NIL,_,_,CONS(h,NIL),_))=empty

It remains to explain how to define a method balance that rebalance the deque if insert' or tail broke the invariant. The method insert and tail can be defined by first applying insert' and tail' and then applying balance.

funbalance(qas(len_front,front,tail_front,len_rear,rear,tail_rear))=letfloor_half_len=(len_front+len_rear)/2inletceil_half_len=len_front+len_rear-floor_half_leniniflen_front>2*len_rear+1thenletvalfront'=take(ceil_half_len,front)valrear'=rotateDrop(rear,floor_half_len,front)in(ceil_half_len,front',front',floor_half_len,rear',rear')elseiflen_front>2*len_rear+1thenletvalrear'=take(floor_half_len,rear)valfront'=rotateDrop(front,ceil_half_len,rear)in(ceil_half_len,front',front',floor_half_len,rear',rear')elseq

where rotateDrop(front, i, rear)) return the concatenation of front and of drop(i, rear). That isfront' = rotateDrop(front, ceil_half_len, rear) put into front' the content of front and the content of rear that is not already in rear'. Since dropping n elements takes ${\displaystyle O(n)}$ time, we use laziness to ensure that elements are dropped two by two, with two drops being done during each tail' and each insert' operation.

funrotateDrop(front,i,rear)=ifi<2thenrotateRev(front,drop(i,rear),NIL)elseletCONS(x,front')=frontinCONS(x,rotateDrop(front',j-2,drop(2,rear)))

where rotateRev(front, middle, rear) is a function that returns the front, followed by the middle reversed, followed by the rear. This function is also defined using laziness to ensure that it can be computed step by step, with one step executed during each insert' and tail' and taking a constant time. This function uses the invariant that |rear|-2|front| is 2 or 3.

funrotateRev(NIL,rear,a)=reverse(rear)++afunrotateRev(CONS(x,front),rear,a)=CONS(x,rotateRev(front,drop(2,rear),reverse(take(2,rear))++a))

where ++ is the function concatenating two lists.

Implementation without laziness

Note that, without the lazy part of the implementation, this would be a non-persistent implementation of queue in O(1) amortized time. In this case, the lists tail_front and tail_rear could be removed from the representation of the double-ended queue.

Language support

Ada's containers provides the generic packages Ada.Containers.Vectors and Ada.Containers.Doubly_Linked_Lists, for the dynamic array and linked list implementations, respectively.

C++'s Standard Template Library provides the class templates std::deque and std::list, for the multiple array and linked list implementations, respectively.

As of Java 6, Java's Collections Framework provides a new Deque interface that provides the functionality of insertion and removal at both ends. It is implemented by classes such as ArrayDeque (also new in Java 6) and LinkedList , providing the dynamic array and linked list implementations, respectively. However, the ArrayDeque, contrary to its name, does not support random access.

Javascript's Array prototype & Perl's arrays have native support for both removing (shift and pop) and adding (unshift and push) elements on both ends.

Python 2.4 introduced the collections module with support for deque objects. It is implemented using a doubly linked list of fixed-length subarrays.

As of PHP 5.3, PHP's SPL extension contains the 'SplDoublyLinkedList' class that can be used to implement Deque datastructures. Previously to make a Deque structure the array functions array_shift/unshift/pop/push had to be used instead.

GHC's Data.Sequence module implements an efficient, functional deque structure in Haskell. The implementation uses 2–3 finger trees annotated with sizes. There are other (fast) possibilities to implement purely functional (thus also persistent) double queues (most using heavily lazy evaluation). ^{[3] [4]} Kaplan and Tarjan were the first to implement optimal confluently persistent catenable deques. ^[5] Their implementation was strictly purely functional in the sense that it did not use lazy evaluation. Okasaki simplified the data structure by using lazy evaluation with a bootstrapped data structure and degrading the performance bounds from worst-case to amortized. ^[6] Kaplan, Okasaki, and Tarjan produced a simpler, non-bootstrapped, amortized version that can be implemented either using lazy evaluation or more efficiently using mutation in a broader but still restricted fashion. ^[7] Mihaescu and Tarjan created a simpler (but still highly complex) strictly purely functional implementation of catenable deques, and also a much simpler implementation of strictly purely functional non-catenable deques, both of which have optimal worst-case bounds. ^[8]

Rust's std::collections includes VecDeque which implements a double-ended queue using a growable ring buffer.

Complexity

• In a doubly-linked list implementation and assuming no allocation/deallocation overhead, the time complexity of all deque operations is O(1). Additionally, the time complexity of insertion or deletion in the middle, given an iterator, is O(1); however, the time complexity of random access by index is O(n).
• In a growing array, the amortized time complexity of all deque operations is O(1). Additionally, the time complexity of random access by index is O(1); but the time complexity of insertion or deletion in the middle is O(n).

Applications

A double-ended queue can be used to store the browsing history: new websites are added to the end of the queue, while the oldest entries will be deleted when the history is too large. When a user asks to clear the browsing history for the past hour, the most recently added entries are removed.

One example where a deque can be used is the work stealing algorithm. ^[9] This algorithm implements task scheduling for several processors. A separate deque with threads to be executed is maintained for each processor. To execute the next thread, the processor gets the first element from the deque (using the "remove first element" deque operation). If the current thread forks, it is put back to the front of the deque ("insert element at front") and a new thread is executed. When one of the processors finishes execution of its own threads (i.e. its deque is empty), it can "steal" a thread from another processor: it gets the last element from the deque of another processor ("remove last element") and executes it. The work stealing algorithm is used by Intel's Threading Building Blocks (TBB) library for parallel programming.

See also

• Pipe
• Priority queue

References

1. Jesse Liberty; Siddhartha Rao; Bradley Jones. C++ in One Hour a Day, Sams Teach Yourself, Sixth Edition. Sams Publishing, 2009. ISBN   0-672-32941-7. Lesson 18: STL Dynamic Array Classes, pp. 486.
2. Donald Knuth. The Art of Computer Programming , Volume 1: Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN   0-201-89683-4. Section 2.2.1: Stacks, Queues, and Deques, pp. 238–243.
3. Okasaki, Chris (September 1996). Purely Functional Data Structures (PDF) (Ph.D. thesis). Carnegie Mellon University. CMU-CS-96-177.
4. Adam L. Buchsbaum and Robert E. Tarjan. Confluently persistent deques via data structural bootstrapping. Journal of Algorithms, 18(3):513–547, May 1995. (pp. 58, 101, 125)
5. Haim Kaplan and Robert E. Tarjan. Purely functional representations of catenable sorted lists. In ACM Symposium on Theory of Computing, pages 202–211, May 1996. (pp. 4, 82, 84, 124)
6. Chris Okasaki (Aug. 1997), Catenable double-ended queues, ACM SIGPLAN Notices Volume 32 Issue 8
7. Haim Kaplan, Chris Okasaki, and Robert E. Tarjan (2000), Simple Confluently Persistent Catenable Lists, SIAM Journal on Computing Vol. 30, Iss. 3
8. Radu Mihaescu and Robert Tarjan (Aug. 2003), Notes on Catenable Deques in Pure Lisp, Princetown University, COS 528, Fall 03
9. Blumofe, Robert D.; Leiserson, Charles E. (1999). "Scheduling multithreaded computations by work stealing" (PDF). J ACM. 46 (5): 720–748. doi:10.1145/324133.324234. S2CID   5428476.

External links

• Type-safe open source deque implementation at Comprehensive C Archive Network
• SGI STL Documentation: deque<T, Alloc>
• Code Project: An In-Depth Study of the STL Deque Container
• Deque implementation in C Archived 2014-03-06 at the Wayback Machine
• VBScript implementation of stack, queue, deque, and Red-Black Tree
• Multiple implementations of non-catenable deques in Haskell