Related Research Articles

In computer science, an AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. That is, it is a k-ary tree with k = 2. A recursive definition using set theory is that a binary tree is a tuple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set containing the root.
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children. Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as databases and file systems.
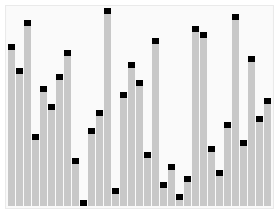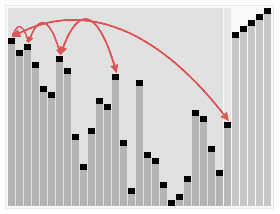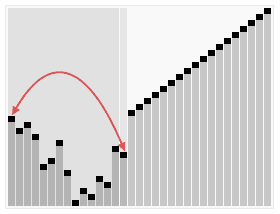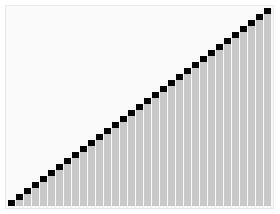
In computer science, heapsort is a comparison-based sorting algorithm which can be thought of as "an implementation of selection sort using the right data structure." Like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to efficiently find the largest element in each step.

In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.
In computer science, a red–black tree is a specialised binary search tree data structure noted for fast storage and retrieval of ordered information, and a guarantee that operations will complete within a known time. Compared to other self-balancing binary search trees, the nodes in a red-black tree hold an extra bit called "color" representing "red" and "black" which is used when re-organising the tree to ensure that it is always approximately balanced.

In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children, but must be connected to exactly one parent, except for the root node, which has no parent. These constraints mean there are no cycles or "loops", and also that each child can be treated like the root node of its own subtree, making recursion a useful technique for tree traversal. In contrast to linear data structures, many trees cannot be represented by relationships between neighboring nodes in a single straight line.

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.
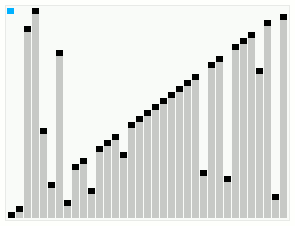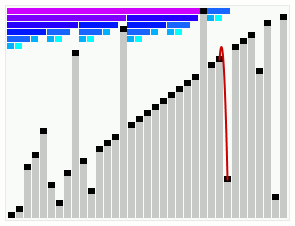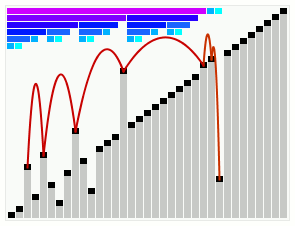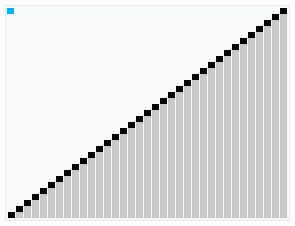
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n) operations (see big O notation), but it is not a stable sort. The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.
In computer science, a binomial heap is a data structure that acts as a priority queue but also allows pairs of heaps to be merged. It is important as an implementation of the mergeable heap abstract data type, which is a priority queue supporting merge operation. It is implemented as a heap similar to a binary heap but using a special tree structure that is different from the complete binary trees used by binary heaps. Binomial heaps were invented in 1978 by Jean Vuillemin.
In computer science, tree traversal is a form of graph traversal and refers to the process of visiting each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.
Adaptive Huffman coding is an adaptive coding technique based on Huffman coding. It permits building the code as the symbols are being transmitted, having no initial knowledge of source distribution, that allows one-pass encoding and adaptation to changing conditions in data.
In computer science, a scapegoat tree is a self-balancing binary search tree, invented by Arne Andersson in 1989 and again by Igal Galperin and Ronald L. Rivest in 1993. It provides worst-case lookup time and amortized insertion and deletion time.
In computer science, a leftist tree or leftist heap is a priority queue implemented with a variant of a binary heap. Every node x has an s-value which is the distance to the nearest leaf in subtree rooted at x. In contrast to a binary heap, a leftist tree attempts to be very unbalanced. In addition to the heap property, leftist trees are maintained so the right descendant of each node has the lower s-value.
A pairing heap is a type of heap data structure with relatively simple implementation and excellent practical amortized performance, introduced by Michael Fredman, Robert Sedgewick, Daniel Sleator, and Robert Tarjan in 1986. Pairing heaps are heap-ordered multiway tree structures, and can be considered simplified Fibonacci heaps. They are considered a "robust choice" for implementing such algorithms as Prim's MST algorithm, and support the following operations :
A skew heap is a heap data structure implemented as a binary tree. Skew heaps are advantageous because of their ability to merge more quickly than binary heaps. In contrast with binary heaps, there are no structural constraints, so there is no guarantee that the height of the tree is logarithmic. Only two conditions must be satisfied:
In computer science, adaptive heap sort is a comparison-based sorting algorithm of the adaptive sort family. It is a variant of heap sort that performs better when the data contains existing order. Published by Christos Levcopoulos and Ola Petersson in 1992, the algorithm utilizes a new measure of presortedness, Osc, as the number of oscillations. Instead of putting all the data into the heap as the traditional heap sort did, adaptive heap sort only take part of the data into the heap so that the run time will reduce significantly when the presortedness of the data is high.

In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.
References
- ↑ Edelkamp, Stefan (26 May 2011), Pieterse, Vreda; Black, Paul E. (eds.), "weak-heap", Dictionary of Algorithms and Data Structures, retrieved 2015-12-01
- 1 2 Edelkamp, Stefan; Elmasry, Amr; Katajainen, Jyrki (October 2012), "The weak-heap data structure: variants and applications" (PDF), Journal of Discrete Algorithms, 16: 187–205, CiteSeerX 10.1.1.455.1213 , doi:10.1016/j.jda.2012.04.010, MR 2960353 .
- 1 2 3 Dutton, Ronald D. (1993), "Weak-heap sort", BIT, 33 (3): 372–381, doi:10.1007/bf01990520 .
- ↑ Bojesen, Jesper; Katajainen, Jyrki; Spork, Maz (2000). "Performance Engineering Case Study: Heap Construction" (PostScript). ACM Journal of Experimental Algorithmics. 5 (15). CiteSeerX 10.1.1.35.3248 . doi:10.1145/351827.384257. Alternate PDF source.
- ↑ Edelkamp, Stefan; Wegener, Ingo (2000), "On the performance of WEAK-HEAPSORT", Stacs 2000 (PDF), Lecture Notes in Computer Science, vol. 1770, Springer-Verlag, pp. 254–266, CiteSeerX 10.1.1.21.1863 , doi:10.1007/3-540-46541-3_21, ISBN 978-3-540-67141-1 .
- ↑ Bruun, Asger; Edelkamp, Stefan; Katajainen, Jyrki; Rasmussen, Jens (2010). "Policy-Based Benchmarking of Weak Heaps and Their Relatives" (PDF). Proceedings of the 9th International Symposium on Experimental Algorithms (SEA 2010). Lecture Notes in Computer Science. Vol. 6049. Springer-Verlag. pp. 424–435. doi:10.1007/978-3-642-13193-6_36. ISBN 978-3-642-13192-9. Archived from the original (PDF) on 2017-08-11..
- Bruun, Asger; Edelkamp, Stefan; Katajainen, Jyrki; Rasmussen, Jens (2010). Policy-Based Benchmarking of Weak Heaps and Their Relatives (PDF). pp. 424–435. doi:10.1007/978-3-642-13193-6_36. ISBN 978-3-642-13192-9. S2CID 1334592. Archived from the original (PDF) on 2016-12-27.
{{cite book}}:|website=ignored (help)
- Bruun, Asger; Edelkamp, Stefan; Katajainen, Jyrki; Rasmussen, Jens (2010). Policy-Based Benchmarking of Weak Heaps and Their Relatives (PDF). pp. 424–435. doi:10.1007/978-3-642-13193-6_36. ISBN 978-3-642-13192-9. S2CID 1334592. Archived from the original (PDF) on 2016-12-27.
- ↑ Edelkamp, Stefan; Elmasry, Amr; Katajainen, Jyrki (2012), "The Weak-heap Family of Priority Queues in Theory and Praxis" (PDF), Proceedings of the Eighteenth Computing: The Australasian Theory Symposium (CATS 2012), vol. 128, Darlinghurst, Australia: Australian Computer Society, Inc., pp. 103–112, ISBN 978-1-921770-09-8 .