Related Research Articles

In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by at most one path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees.

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node and explores as far as possible along each branch before backtracking. Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph.

In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to information science to computation (scheduling).

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges.
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u,v) from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance or shortest-path distance. Notice that there may be more than one shortest path between two vertices. If there is no path connecting the two vertices, i.e., if they belong to different connected components, then conventionally the distance is defined as infinite.

In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or forest. It is equal to the number of independent cycles in the graph. Unlike the corresponding feedback arc set problem for directed graphs, the circuit rank r is easily computed using the formula
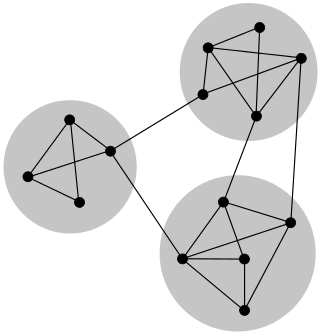
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.
In the mathematical field of graph theory, a transitive reduction of a directed graph D is another directed graph with the same vertices and as few edges as possible, such that for all pairs of vertices v, w a (directed) path from v to w in D exists if and only if such a path exists in the reduction. Transitive reductions were introduced by Aho, Garey & Ullman (1972), who provided tight bounds on the computational complexity of constructing them.
In computer science, Kosaraju-Sharir's algorithm is a linear time algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to S. Rao Kosaraju and Micha Sharir. Kosaraju suggested it in 1978 but did not publish it, while Sharir independently discovered it and published it in 1981. It makes use of the fact that the transpose graph has exactly the same strongly connected components as the original graph.
In computer science, graph traversal refers to the process of visiting each vertex in a graph. Such traversals are classified by the order in which the vertices are visited. Tree traversal is a special case of graph traversal.

In mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by directed edges, often called arcs.
In graph theory, a Trémaux tree of an undirected graph is a type of spanning tree, generalizing depth-first search trees. They are defined by the property that every edge of connects an ancestor–descendant pair in the tree. Trémaux trees are named after Charles Pierre Trémaux, a 19th-century French author who used a form of depth-first search as a strategy for solving mazes. They have also been called normal spanning trees, especially in the context of infinite graphs.
In the mathematics of infinite graphs, an end of a graph represents, intuitively, a direction in which the graph extends to infinity. Ends may be formalized mathematically as equivalence classes of infinite paths, as havens describing strategies for pursuit–evasion games on the graph, or as topological ends of topological spaces associated with the graph.
In graph theory, a bipolar orientation or st-orientation of an undirected graph is an assignment of a direction to each edge that causes the graph to become a directed acyclic graph with a single source s and a single sink t, and an st-numbering of the graph is a topological ordering of the resulting directed acyclic graph.
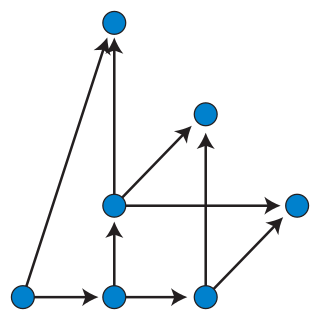
Dominance drawing is a style of graph drawing of directed acyclic graphs that makes the reachability relations between vertices visually apparent. In dominance drawing, vertices are placed at distinct points of the Euclidean plane and a vertex v is reachable from another vertex u if and only if both Cartesian coordinates of v are greater than or equal to the coordinates of u. The edges of a dominance drawing may be drawn either as straight line segments, or, in some cases, as polygonal chains.
In graph theory, the weak components of a directed graph partition the vertices of the graph into subsets that are totally ordered by reachability. They form the finest partition of the set of vertices that is totally ordered in this way.
References
- 1 2 Schrijver, Alexander (2002-12-10). Combinatorial Optimization: Polyhedra and Efficiency. Springer Science & Business Media. p. 89. ISBN 9783540443896.
- ↑ Sedgewick, Robert; Wayne, Kevin (2016-09-26). "Directed Graphs". Algorithms, 4th Edition. Retrieved 2017-09-06.