In computer science, an AVL tree is a self-balancing binary search tree (BST). It was the first such data structure to be invented. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is directly proportional to the height of the tree.
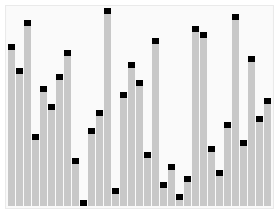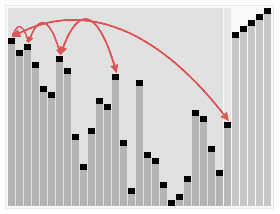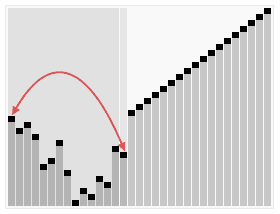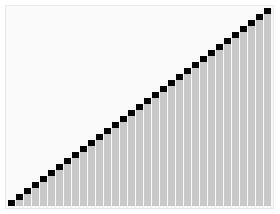
In computer science, heapsort is a comparison-based sorting algorithm. Heapsort can be thought of as an improved selection sort: like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to more quickly find the largest element in each step.

In computer science, a heap is a specialized tree-based data structure which is essentially an almost complete tree that satisfies the heap property: in a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.
Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

In computer science, merge sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.
In computer science, a priority queue is an abstract data-type similar to a regular queue or stack data structure in which each element additionally has a "priority" associated with it. In a priority queue, an element with high priority is served before an element with low priority. In some implementations, if two elements have the same priority, they are served according to the order in which they were enqueued; in other implementations ordering of elements with the same priority remains undefined.
A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For random access patterns drawn from a non-uniform random distribution, their amortized time can be faster than logarithmic, proportional to the entropy of the access pattern. For many patterns of non-random operations, also, splay trees can take better than logarithmic time, without requiring advance knowledge of the pattern. According to the unproven dynamic optimality conjecture, their performance on all access patterns is within a constant factor of the best possible performance that could be achieved by any other self-adjusting binary search tree, even one selected to fit that pattern. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.
In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n), but it is not a stable sort. The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.
Introsort or introspective sort is a hybrid sorting algorithm that provides both fast average performance and (asymptotically) optimal worst-case performance. It begins with quicksort, it switches to heapsort when the recursion depth exceeds a level based on the number of elements being sorted and it switches to insertion sort when the number of elements is below some threshold. This combines the good parts of the three algorithms, with practical performance comparable to quicksort on typical data sets and worst-case O(n log n) runtime due to the heap sort. Since the three algorithms it uses are comparison sorts, it is also a comparison sort.

In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. These operations when designed for a self-balancing binary search tree, contain precautionary measures against boundlessly increasing tree height, so that these abstract data structures receive the attribute "self-balancing".

In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are a useful data structure for several applications, such as searches involving a multidimensional search key and creating point clouds. k-d trees are a special case of binary space partitioning trees.

A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list. The only requirement is that the operator forms a total preorder over the data, with:
- if a ≤ b and b ≤ c then a ≤ c (transitivity)
- for all a and b, a ≤ b or b ≤ a (connexity).

Quicksort is an in-place sorting algorithm. Developed by British computer scientist Tony Hoare in 1959 and published in 1961, it is still a commonly used algorithm for sorting. When implemented well, it can be somewhat faster than merge sort and about two or three times faster than heapsort.

In computer science, a Cartesian tree is a binary tree derived from a sequence of numbers; it can be uniquely defined from the properties that it is heap-ordered and that a symmetric (in-order) traversal of the tree returns the original sequence. Introduced by Vuillemin (1980) in the context of geometric range searching data structures, Cartesian trees have also been used in the definition of the treap and randomized binary search tree data structures for binary search problems. The Cartesian tree for a sequence may be constructed in linear time using a stack-based algorithm for finding all nearest smaller values in a sequence.
A sorted array is an array data structure in which each element is sorted in numerical, alphabetical, or some other order, and placed at equally spaced addresses in computer memory. It is typically used in computer science to implement static lookup tables to hold multiple values which have the same data type. Sorting an array is useful in organising data in ordered form and recovering them rapidly.