Proportion extend sort

Last updated
Proportion extend sort
Class Sorting algorithm
Data structure Array
Worst-case performance O(n log n)
Best-case performance O(n log n)
Average performance O(n log n)
Worst-case space complexity O(log n) auxiliary
OptimalYes

Proportion extend sort (abbreviated as PESort) is an in-place, comparison-based sorting algorithm which attempts to improve on the performance, particularly the worst-case performance, of quicksort.

Contents

The basic partitioning operation in quicksort has a linear access pattern which is extremely efficient on modern memory hierarchies, but the performance of the algorithm is critically dependent on the choice of a pivot value. A good pivot will divide the data to be sorted into nearly equal halves. A poor choice will result in a grossly lopsided division, leaving one part almost as large as the original problem and causing O(n2) performance.

Proportion extend sort begins with a sorted prefix of k elements, then uses the median of that sample to partition the following pk elements. By bounding the size ratio p between the sample and the data being partitioned (i.e. the proportion by which the sorted prefix is extended), the imbalance is limited. In this, it has some similarities to samplesort. [1]

History

Proportion extend sort was published by Jing-Chao Chen in 2001 [2] as an improvement on his earlier proportion split sort design. [3] Its average-case performance, which was only experimentally measured in the original paper, was analyzed by Richard Cole and David C. Kandathil in 2004 [4] and by Chen in 2006, [5] and shown to require log2n + O(n) comparisons on average. A slightly refined variant, symmetry partition sort, was published in 2007. [6]

Algorithm

The algorithm begins with an array divided into a sorted part S adjacent to an unsorted part U. (The original proportion extend sort always had the sorted part precede the unsorted part; the symmetric variant allows either order.) It is possible to begin with the first element as the sorted part (a single element is always sorted), or to sort a small number of elements using a simpler insertion sort. The initially sorted elements may also be taken from across the array to improve performance in the case of pre-sorted data.

Next, and most critically, the length of the unsorted part |U| is bounded to a multiple p of the length of the sorted part |S|. Specifically, if |U| > p2|S|, then recursively sort S and the adjacent p|S| elements of U, make the result (p+1 times longer than the original [a] ) the new S, and repeat until the condition is satisfied.

If there is no limit on the unsorted part (p=∞), then the algorithm is equivalent to quicksort. If the unsorted part is of length 1 (p=0, almost), then the algorithm is equivalent to binary insertion sort. Values around p≈16 give the best average-case performance, competitive with quicksort, [6] : 764  while smaller values improve worst-case performance. [b]

Eliezer Albacea published a similar algorithm in 1995 called Leapfrogging samplesort where the size is limited so |U| ≤ |S|+1, [7] [1] later generalized to (2k−1)(|S|+1). [8]

The sorted part of the array is divided in half (at the median), and one half is moved (by exchanging it with unsorted elements) to the far end of the array, so we have an initial partially partitioned array of the form LUR, where L is the left half of the sorted part, U is the bounded-length unsorted part, and R is the right half of the sorted part.

Then the standard quicksort partitioning step is performed on U, dividing it (in place) into UL and UR. UL and UR are not sorted, but every element of UL is less than or equal to the median, and every element of UR is greater or equal. [c] The final result LULURR consists of two arrays of the necessary form (a sorted part adjacent to an unsorted part) and are sorted recursively.

Leapfrogging samplesort and the original proportion extend sort have the sorted part always precede the unsorted part, achieved by partitioning Ubefore moving R, resulting in LRULUR, and then exchanging R with the end of UL, resulting in LULRUR. While the symmetric version is a bit trickier, it has the advantage that the L and R parts act as sentinel values for the partitioning loops, eliminating the need to test in the loop if the bounds of U have been reached.

Most of the implementation refinements used for quicksort can be applied, including techniques for detecting and efficiently handling mostly sorted inputs. [9] [6] In particular, sub-sorts below a certain size threshold are usually implemented using a simple insertion sort.

As with quicksort, the number of recursive levels can be limited to log2n if the smaller sub-sort is done first and the larger is implemented as a tail call. Unlike quicksort, the number of levels is bounded by O(log n) even if this is not done. [9] : 781 

Notes

  1. ↑ Note that different sources use different conventions for p: Chen uses the ratio of the unsorted part to the sorted part, so any p>0 makes sense, while others have it as the ratio of the total size to that of the sorted part, so only p>1 makes sense.
  2. ↑ The algorithm requires at most 1/log2(1 + 1/(2p2+2p−1)) n log2n comparisons. For p ≤ 16, that constant may be approximated by 1.37p2+1.63p−0.5.
  3. ↑ This assumes an ascending sort. A descending sort requires the obvious adjustments.

Related Research Articles

<span class="mw-page-title-main">Heapsort</span> A sorting algorithm which uses the heap data structure

In computer science, heapsort is a comparison-based sorting algorithm which can be thought of as "an implementation of selection sort using the right data structure." Like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to efficiently find the largest element in each step.

<span class="mw-page-title-main">Insertion sort</span> Sorting algorithm

Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

<span class="mw-page-title-main">Merge sort</span> Divide and conquer sorting algorithm

In computer science, Merge Sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the relative order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.

Merge algorithms are a family of algorithms that take multiple sorted lists as input and produce a single list as output, containing all the elements of the inputs lists in sorted order. These algorithms are used as subroutines in various sorting algorithms, most famously merge sort.

In computer science, radix sort is a non-comparative sorting algorithm. It avoids comparison by creating and distributing elements into buckets according to their radix. For elements with more than one significant digit, this bucketing process is repeated for each digit, while preserving the ordering of the prior step, until all digits have been considered. For this reason, radix sort has also been called bucket sort and digital sort.

<span class="mw-page-title-main">Sorting algorithm</span> Algorithm that arranges lists in order

In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.

<span class="mw-page-title-main">Bucket sort</span> Sorting algorithm

Bucket sort, or bin sort, is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, a generalization of pigeonhole sort that allows multiple keys per bucket, and is a cousin of radix sort in the most-to-least significant digit flavor. Bucket sort can be implemented with comparisons and therefore can also be considered a comparison sort algorithm. The computational complexity depends on the algorithm used to sort each bucket, the number of buckets to use, and whether the input is uniformly distributed.

Introsort or introspective sort is a hybrid sorting algorithm that provides both fast average performance and (asymptotically) optimal worst-case performance. It begins with quicksort, it switches to heapsort when the recursion depth exceeds a level based on (the logarithm of) the number of elements being sorted and it switches to insertion sort when the number of elements is below some threshold. This combines the good parts of the three algorithms, with practical performance comparable to quicksort on typical data sets and worst-case O(n log n) runtime due to the heap sort. Since the three algorithms it uses are comparison sorts, it is also a comparison sort.

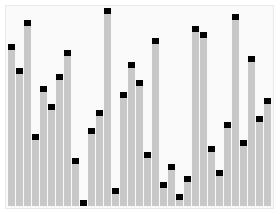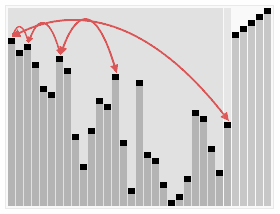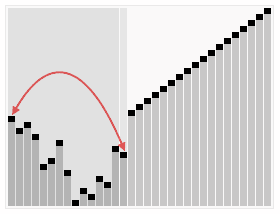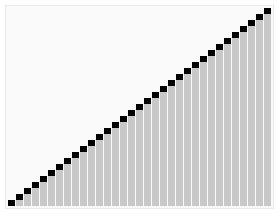
In computer science, a selection algorithm is an algorithm for finding the th smallest value in a collection of ordered values, such as numbers. The value that it finds is called the th order statistic. Selection includes as special cases the problems of finding the minimum, median, and maximum element in the collection. Selection algorithms include quickselect, and the median of medians algorithm. When applied to a collection of values, these algorithms take linear time, as expressed using big O notation. For data that is already structured, faster algorithms may be possible; as an extreme case, selection in an already-sorted array takes time .

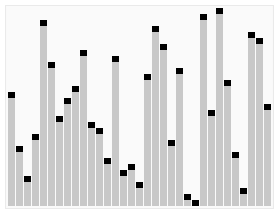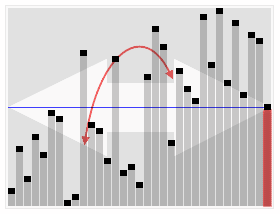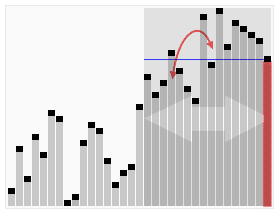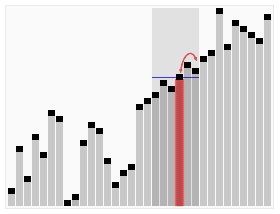
<span class="mw-page-title-main">Quickselect</span> Algorithm for the kth smallest element in an array

In computer science, quickselect is a selection algorithm to find the kth smallest element in an unordered list, also known as the kth order statistic. Like the related quicksort sorting algorithm, it was developed by Tony Hoare, and thus is also known as Hoare's selection algorithm. Like quicksort, it is efficient in practice and has good average-case performance, but has poor worst-case performance. Quickselect and its variants are the selection algorithms most often used in efficient real-world implementations.

<span class="mw-page-title-main">Quicksort</span> Divide and conquer sorting algorithm

Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.

sort is a generic function in the C++ Standard Library for doing comparison sorting. The function originated in the Standard Template Library (STL).

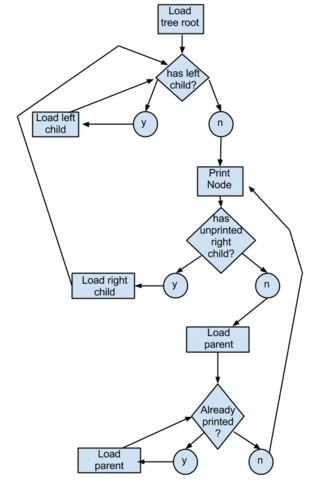
<span class="mw-page-title-main">Tree sort</span> Type of sorting algorithm

A tree sort is a sort algorithm that builds a binary search tree from the elements to be sorted, and then traverses the tree (in-order) so that the elements come out in sorted order. Its typical use is sorting elements online: after each insertion, the set of elements seen so far is available in sorted order.

Spreadsort is a sorting algorithm invented by Steven J. Ross in 2002. It combines concepts from distribution-based sorts, such as radix sort and bucket sort, with partitioning concepts from comparison sorts such as quicksort and mergesort. In experimental results it was shown to be highly efficient, often outperforming traditional algorithms such as quicksort, particularly on distributions exhibiting structure and string sorting. There is an open-source implementation with performance analysis and benchmarks, and HTML documentation .

Samplesort is a sorting algorithm that is a divide and conquer algorithm often used in parallel processing systems. Conventional divide and conquer sorting algorithms partitions the array into sub-intervals or buckets. The buckets are then sorted individually and then concatenated together. However, if the array is non-uniformly distributed, the performance of these sorting algorithms can be significantly throttled. Samplesort addresses this issue by selecting a sample of size s from the n-element sequence, and determining the range of the buckets by sorting the sample and choosing p−1 < s elements from the result. These elements then divide the array into p approximately equal-sized buckets. Samplesort is described in the 1970 paper, "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W. D. Frazer and A. C. McKellar.

In computer science, partial sorting is a relaxed variant of the sorting problem. Total sorting is the problem of returning a list of items such that its elements all appear in order, while partial sorting is returning a list of the k smallest elements in order. The other elements may also be sorted, as in an in-place partial sort, or may be discarded, which is common in streaming partial sorts. A common practical example of partial sorting is computing the "Top 100" of some list.

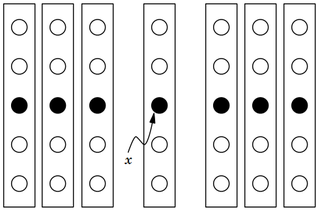
<span class="mw-page-title-main">Median of medians</span> Fast approximate median algorithm

In computer science, the median of medians is an approximate median selection algorithm, frequently used to supply a good pivot for an exact selection algorithm, most commonly quickselect, that selects the kth smallest element of an initially unsorted array. Median of medians finds an approximate median in linear time. Using this approximate median as an improved pivot, the worst-case complexity of quickselect reduces from quadratic to linear, which is also the asymptotically optimal worst-case complexity of any selection algorithm. In other words, the median of medians is an approximate median-selection algorithm that helps building an asymptotically optimal, exact general selection algorithm, by producing good pivot elements.

The cache-oblivious distribution sort is a comparison-based sorting algorithm. It is similar to quicksort, but it is a cache-oblivious algorithm, designed for a setting where the number of elements to sort is too large to fit in a cache where operations are done. In the external memory model, the number of memory transfers it needs to perform a sort of items on a machine with cache of size and cache lines of length is , under the tall cache assumption that . This number of memory transfers has been shown to be asymptotically optimal for comparison sorts. This distribution sort also achieves the asymptotically optimal runtime complexity of .

Multi-key quicksort, also known as three-way radix quicksort, is an algorithm for sorting strings. This hybrid of quicksort and radix sort was originally suggested by P. Shackleton, as reported in one of C.A.R. Hoare's seminal papers on quicksort; its modern incarnation was developed by Jon Bentley and Robert Sedgewick in the mid-1990s. The algorithm is designed to exploit the property that in many problems, strings tend to have shared prefixes.

References

  1. 1 2 Albacea, Eliezer A. (January 2012). "Average-case analysis of Leapfrogging samplesort" (PDF). Philippine Science Letters. 5 (1).
  2. ↑ Chen, Jing-Chao (July 2001). "Proportion extend sort". SIAM Journal on Computing . 31 (1): 323–330. doi:10.1137/S0097539798342903.
  3. ↑ Chen, Jing-Chao (Fall 1996). "Proportion Extend Sort". SIAM Journal on Computing. 3 (3): 271–279. doi:10.1137/S0097539798342903.
  4. ↑ Cole, Richard; Kandathil, David C. (14–17 September 2004). The Average Case Analysis of Partition Sorts (PDF). Algorithms—ESA 2004: 12th Annual European Symposium. Bergen. pp. 240–251. doi:10.1007/978-3-540-30140-0_23. ISBN   3-540-23025-4.
  5. ↑ Chen, Jing-Chao (15 December 2006). "Efficient sample sort and the average case analysis of PEsort". Theoretical Computer Science. 369 (1–3): 44–66. doi: 10.1016/j.tcs.2006.07.017 .
  6. 1 2 3 Chen, Jing-Chao (11 September 2007). "Symmetry Partition Sort". Software: Practice and Experience. 38 (7): 761–773. arXiv: 0706.0046 . doi:10.1002/spe.851. S2CID   844616.
  7. ↑ Albacea, Eliezer A. (1995). Leapfrogging samplesort. Asian Computing Science Conference. doi:10.1007/3-540-60688-2_30.
  8. ↑ Albacea, Eliezer A. (29 January 2018). "Generalized Leapfrogging Samplesort: A Class of O(n log22 n) Worst-Case Complexity and O(n log n) Average-Case Complexity Sorting Algorithms". arXiv: 1801.09431 [cs.DS].
  9. 1 2 Chen, Jing-Chao (10 July 2004). "Building a new sort function for a C library". Software: Practice and Experience. 34 (8): 777–795. doi:10.1002/spe.593. S2CID   8193225.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.