Pancake sorting is the mathematical problem of sorting a disordered stack of pancakes in order of size when a spatula can be inserted at any point in the stack and used to flip all pancakes above it. A pancake number is the minimum number of flips required for a given number of pancakes. In this form, the problem was first discussed by American geometer Jacob E. Goodman. [1] A variant of the problem is concerned with burnt pancakes, where each pancake has a burnt side and all pancakes must, in addition, end up with the burnt side on the bottom.
Contents
- The pancake problems
- The original pancake problem
- The burnt pancake problem
- The pancake problem on strings
- History
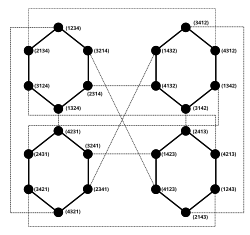
- Pancake graphs
- Algorithm
- Related integer sequences
- References
- Further reading
- External links
All sorting methods require pairs of elements to be compared. For the traditional sorting problem, the usual problem studied is to minimize the number of comparisons required to sort a list. The number of actual operations, such as swapping two elements, is then irrelevant. For pancake sorting problems, in contrast, the aim is to minimize the number of operations, where the only allowed operations are reversals of the elements of some prefix of the sequence. Now, the number of comparisons is irrelevant.