
In computer science, an AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.
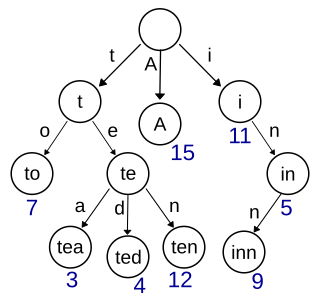
In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.
In computer science, a skip list is a probabilistic data structure that allows average complexity for search as well as average complexity for insertion within an ordered sequence of elements. Thus it can get the best features of a sorted array while maintaining a linked list-like structure that allows insertion, which is not possible with a static array. Fast search is made possible by maintaining a linked hierarchy of subsequences, with each successive subsequence skipping over fewer elements than the previous one. Searching starts in the sparsest subsequence until two consecutive elements have been found, one smaller and one larger than or equal to the element searched for. Via the linked hierarchy, these two elements link to elements of the next sparsest subsequence, where searching is continued until finally searching in the full sequence. The elements that are skipped over may be chosen probabilistically or deterministically, with the former being more common.
In computing, a persistent data structure or not ephemeral data structure is a data structure that always preserves the previous version of itself when it is modified. Such data structures are effectively immutable, as their operations do not (visibly) update the structure in-place, but instead always yield a new updated structure. The term was introduced in Driscoll, Sarnak, Sleator, and Tarjans' 1986 article.
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets, and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets.
A B+ tree is an m-ary tree with a variable but often large number of children per node. A B+ tree consists of a root, internal nodes and leaves. The root may be either a leaf or a node with two or more children.
In data processing R*-trees are a variant of R-trees used for indexing spatial information. R*-trees have slightly higher construction cost than standard R-trees, as the data may need to be reinserted; but the resulting tree will usually have a better query performance. Like the standard R-tree, it can store both point and spatial data. It was proposed by Norbert Beckmann, Hans-Peter Kriegel, Ralf Schneider, and Bernhard Seeger in 1990.
In computer science, an interval tree is a tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point. It is often used for windowing queries, for instance, to find all roads on a computerized map inside a rectangular viewport, or to find all visible elements inside a three-dimensional scene. A similar data structure is the segment tree.
In computer science, weight-balanced binary trees (WBTs) are a type of self-balancing binary search trees that can be used to implement dynamic sets, dictionaries (maps) and sequences. These trees were introduced by Nievergelt and Reingold in the 1970s as trees of bounded balance, or BB[α] trees. Their more common name is due to Knuth.
In graph theory and computer science, the lowest common ancestor (LCA) of two nodes v and w in a tree or directed acyclic graph (DAG) T is the lowest node that has both v and w as descendants, where we define each node to be a descendant of itself.
In computer science, fractional cascading is a technique to speed up a sequence of binary searches for the same value in a sequence of related data structures. The first binary search in the sequence takes a logarithmic amount of time, as is standard for binary searches, but successive searches in the sequence are faster. The original version of fractional cascading, introduced in two papers by Chazelle and Guibas in 1986, combined the idea of cascading, originating in range searching data structures of Lueker (1978) and Willard (1978), with the idea of fractional sampling, which originated in Chazelle (1983). Later authors introduced more complex forms of fractional cascading that allow the data structure to be maintained as the data changes by a sequence of discrete insertion and deletion events.
In computer science, a succinct data structure is a data structure which uses an amount of space that is "close" to the information-theoretic lower bound, but still allows for efficient query operations. The concept was originally introduced by Jacobson to encode bit vectors, (unlabeled) trees, and planar graphs. Unlike general lossless data compression algorithms, succinct data structures retain the ability to use them in-place, without decompressing them first. A related notion is that of a compressed data structure, insofar as the size of the stored or encoded data similarly depends upon the specific content of the data itself.

A top tree is a data structure based on a binary tree for unrooted dynamic trees that is used mainly for various path-related operations. It allows simple divide-and-conquer algorithms. It has since been augmented to maintain dynamically various properties of a tree such as diameter, center and median.
Skip graphs are a kind of distributed data structure based on skip lists. They were invented in 2003 by James Aspnes and Gauri Shah. A nearly identical data structure called SkipNet was independently invented by Nicholas Harvey, Michael Jones, Stefan Saroiu, Marvin Theimer and Alec Wolman, also in 2003.

In computer science, the log-structured merge-tree is a data structure with performance characteristics that make it attractive for providing indexed access to files with high insert volume, such as transactional log data. LSM trees, like other search trees, maintain key-value pairs. LSM trees maintain data in two or more separate structures, each of which is optimized for its respective underlying storage medium; data is synchronized between the two structures efficiently, in batches.
The PH-tree is a tree data structure used for spatial indexing of multi-dimensional data (keys) such as geographical coordinates, points, feature vectors, rectangles or bounding boxes. The PH-tree is space partitioning index with a structure similar to that of a quadtree or octree. However, unlike quadtrees, it uses a splitting policy based on tries and similar to Crit bit trees that is based on the bit-representation of the keys. The bit-based splitting policy, when combined with the use of different internal representations for nodes, provides scalability with high-dimensional data. The bit-representation splitting policy also imposes a maximum depth, thus avoiding degenerated trees and the need for rebalancing.



































