Related Research Articles

In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. That is, it is a k-ary tree with k = 2. A recursive definition using set theory is that a binary tree is a tuple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set containing the root.
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children. Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as databases and file systems.
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that data access time is linear in respect to the number of nodes in the list. Because nodes are serially linked, accessing any node requires that the prior node be accessed beforehand. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.
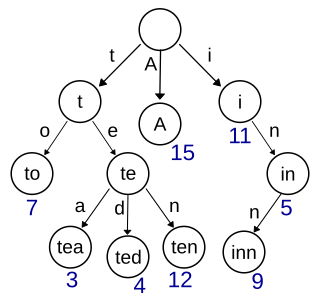
In computer science, a trie, also called digital tree or prefix tree, is a type of search tree: specifically, a k-ary tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.
In computer science, a Fibonacci heap is a data structure for priority queue operations, consisting of a collection of heap-ordered trees. It has a better amortized running time than many other priority queue data structures including the binary heap and binomial heap. Michael L. Fredman and Robert E. Tarjan developed Fibonacci heaps in 1984 and published them in a scientific journal in 1987. Fibonacci heaps are named after the Fibonacci numbers, which are used in their running time analysis.

R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons. The R-tree was proposed by Antonin Guttman in 1984 and has found significant use in both theoretical and applied contexts. A common real-world usage for an R-tree might be to store spatial objects such as restaurant locations or the polygons that typical maps are made of: streets, buildings, outlines of lakes, coastlines, etc. and then find answers quickly to queries such as "Find all museums within 2 km of my current location", "retrieve all road segments within 2 km of my location" or "find the nearest gas station". The R-tree can also accelerate nearest neighbor search for various distance metrics, including great-circle distance.
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets, and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets.
A B+ tree is an m-ary tree with a variable but often large number of children per node. A B+ tree consists of a root, internal nodes and leaves. The root may be either a leaf or a node with two or more children.

In computer science a T-tree is a type of binary tree data structure that is used by main-memory databases, such as Datablitz, eXtremeDB, MySQL Cluster, Oracle TimesTen and MobileLite.
In data processing R*-trees are a variant of R-trees used for indexing spatial information. R*-trees have slightly higher construction cost than standard R-trees, as the data may need to be reinserted; but the resulting tree will usually have a better query performance. Like the standard R-tree, it can store both point and spatial data. It was proposed by Norbert Beckmann, Hans-Peter Kriegel, Ralf Schneider, and Bernhard Seeger in 1990.
In computer science, an interval tree is a tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point. It is often used for windowing queries, for instance, to find all roads on a computerized map inside a rectangular viewport, or to find all visible elements inside a three-dimensional scene. A similar data structure is the segment tree.

In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. K-dimensional is that which concerns exactly k orthogonal axes or a space of any number of dimensions. k-d trees are a useful data structure for several applications, such as:

In mathematical analysis and computer science, functions which are Z-order, Lebesgue curve, Morton space-filling curve, Morton order or Morton code map multidimensional data to one dimension while preserving locality of the data points. It is named in France after Henri Lebesgue, who studied it in 1904, and named in the United States after Guy Macdonald Morton, who first applied the order to file sequencing in 1966. The z-value of a point in multidimensions is simply calculated by interleaving the binary representations of its coordinate values. Once the data are sorted into this ordering, any one-dimensional data structure can be used, such as simple one dimensional arrays, binary search trees, B-trees, skip lists or hash tables. The resulting ordering can equivalently be described as the order one would get from a depth-first traversal of a quadtree or octree.

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.
The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.
In computer science, weight-balanced binary trees (WBTs) are a type of self-balancing binary search trees that can be used to implement dynamic sets, dictionaries (maps) and sequences. These trees were introduced by Nievergelt and Reingold in the 1970s as trees of bounded balance, or BB[α] trees. Their more common name is due to Knuth.
A link/cut tree is a data structure for representing a forest, a set of rooted trees, and offers the following operations:
Hilbert R-tree, an R-tree variant, is an index for multidimensional objects such as lines, regions, 3-D objects, or high-dimensional feature-based parametric objects. It can be thought of as an extension to B+-tree for multidimensional objects.
The Priority R-tree is a worst-case asymptotically optimal alternative to the spatial tree R-tree. It was first proposed by Arge, De Berg, Haverkort and Yi, K. in an article from 2004. The prioritized R-tree is essentially a hybrid between a k-dimensional tree and a R-tree in that it defines a given object's N-dimensional bounding volume as a point in N-dimensions, represented by the ordered pair of the rectangles. The term prioritized arrives from the introduction of four priority-leaves that represents the most extreme values of each dimensions, included in every branch of the tree. Before answering a window-query by traversing the sub-branches, the prioritized R-tree first checks for overlap in its priority nodes. The sub-branches are traversed by checking whether the least value of the first dimension of the query is above the value of the sub-branches. This gives access to a quick indexation by the value of the first dimension of the bounding box.
In computer science, a K-D-B-tree (k-dimensional B-tree) is a tree data structure for subdividing a k-dimensional search space. The aim of the K-D-B-tree is to provide the search efficiency of a balanced k-d tree, while providing the block-oriented storage of a B-tree for optimizing external memory accesses.
The PH-tree is a tree data structure used for spatial indexing of multi-dimensional data (keys) such as geographical coordinates, points, feature vectors, rectangles or bounding boxes. The PH-tree is space partitioning index with a structure similar to that of a quadtree or octree. However, unlike quadtrees, it uses a splitting policy based on tries and similar to Crit bit trees that is based on the bit-representation of the keys. The bit-based splitting policy, when combined with the use of different internal representations for nodes, provides scalability with high-dimensional data. The bit-representation splitting policy also imposes a maximum depth, thus avoiding degenerated trees and the need for rebalancing.
References
- ↑ Selçuk Candan, K.; Luisa Sapino, Maria (31 May 2010). Cambridge University Press (ed.). Data Management for Multimedia Retrieval. Cambridge University Press. ISBN 9781139489584.
- ↑ Berchtold, Stefan; Keim, Daniel A.; Kriegel, Hans-Peter (1996). "The X-tree: An Index Structure for High-Dimensional Data". Proceedings of the 22nd VLDB Conference. Mumbai, India: 28–39.