 |
A concurrent hash-trie or Ctrie [1] [2] is a concurrent thread-safe lock-free implementation of a hash array mapped trie. It is used to implement the concurrent map abstraction. It has particularly scalable concurrent insert and remove operations and is memory-efficient. [3] It is the first known concurrent data-structure that supports O(1), atomic, lock-free snapshots. [2] [4]
The Ctrie data structure is a non-blocking concurrent hash array mapped trie based on single-word compare-and-swap instructions in a shared-memory system. It supports concurrent lookup, insert and remove operations. Just like the hash array mapped trie, it uses the entire 32-bit space for hash values thus having low risk of hashcode collisions. Each node may have up to 32 sub-nodes, but to conserve memory, the list of sub-nodes is represented by a 32-bit bitmap where each bit indicates the presence of a branch, followed by a non-sparse array (of pointers to sub-nodes) whose length equals the Hamming weight of the bitmap.
Keys are inserted by doing an atomic compare-and-swap operation on the node which needs to be modified. To ensure that updates are done independently and in a proper order, a special indirection node (an I-node) is inserted between each regular node and its subtries[ check spelling ].
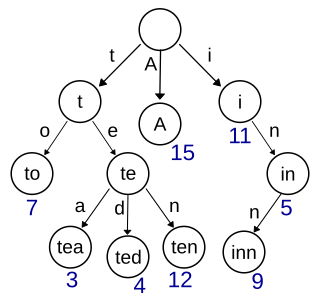
The figure above illustrates the Ctrie insert operation. Trie A is empty - an atomic CAS instruction is used to swap the old node C1 with the new version of C1 which has the new key k1. If the CAS is not successful, the operation is restarted. If the CAS is successful, we obtain the trie B. This procedure is repeated when a new key k2 is added (trie C). If two hashcodes of the keys in the Ctrie collide as is the case with k2 and k3, the Ctrie must be extended with at least one more level - trie D has a new indirection node I2 with a new node C2 which holds both colliding keys. Further CAS instructions are done on the contents of the indirection nodes I1 and I2 - such CAS instructions can be done independently of each other, thus enabling concurrent updates with less contention.
The Ctrie is defined by the pointer to the root indirection node (or a root I-node). The following types of nodes are defined for the Ctrie:
structure INode { main: CNode } structure CNode { bmp: integer array: Branch[2^W] } Branch: INode | SNode structure SNode { k: KeyType v: ValueType }A C-node is a branching node. It typically contains up to 32 branches, so W above is 5. Each branch may either be a key-value pair (represented with an S-node) or another I-node. To avoid wasting 32 entries in the branching array when some branches may be empty, an integer bitmap is used to denote which bits are full and which are empty. The helper method flagpos is used to inspect the relevant hashcode bits for a given level and extract the value of the bit in the bitmap to see if its set or not - denoting whether there is a branch at that position or not. If there is a bit, it also computes its position in the branch array. The formula used to do this is:
bit = bmp & (1 << ((hashcode >> level) & 0x1F)) pos = bitcount((bit - 1) & bmp)
Note that the operations treat only the I-nodes as mutable nodes - all other nodes are never changed after being created and added to the Ctrie.
Below is an illustration of the pseudocode of the insert operation:
definsert(k,v)r=READ(root)ifiinsert(r,k,v,0,null)=RESTARTinsert(k,v)defiinsert(i,k,v,lev,parent)cn=READ(i.main)flag,pos=flagpos(k.hc,lev,cn.bmp)ifcn.bmp&flag=0{ncn=cn.inserted(pos,flag,SNode(k,v))ifCAS(i.main,cn,ncn)returnOKelsereturnRESTART}cn.array(pos)match{casesin:INode=>{returniinsert(sin,k,v,lev+W,i)casesn:SNode=>ifsn.k≠k{nsn=SNode(k,v)nin=INode(CNode(sn,nsn,lev+W))ncn=cn.updated(pos,nin)ifCAS(i.main,cn,ncn)returnOKelsereturnRESTART}else{ncn=cn.updated(pos,SNode(k,v))ifCAS(i.main,cn,ncn)returnOKelsereturnRESTART}}The inserted and updated methods on nodes return new versions of the C-node with a value inserted or updated at the specified position, respectively. Note that the insert operation above is tail-recursive, so it can be rewritten as a while loop. Other operations are described in more detail in the original paper on Ctries. [1] [5]
The data-structure has been proven to be correct [1] - Ctrie operations have been shown to have the atomicity, linearizability and lock-freedom properties. The lookup operation can be modified to guarantee wait-freedom.
Ctries have been shown to be comparable in performance with concurrent skip lists, [2] [4] concurrent hash tables and similar data structures in terms of the lookup operation, being slightly slower than hash tables and faster than skip lists due to the lower level of indirections. However, they are far more scalable than most concurrent hash tables where the insertions are concerned. [1] Most concurrent hash tables are bad at conserving memory - when the keys are removed from the hash table, the underlying array is not shrunk. Ctries have the property that the allocated memory is always a function of only the current number of keys in the data-structure. [1]
Ctries have logarithmic complexity bounds of the basic operations, albeit with a low constant factor due to the high branching level (usually 32).
Ctries support a lock-free, linearizable, constant-time snapshot operation, [2] based on the insight obtained from persistent data structures. This is a breakthrough in concurrent data-structure design, since existing concurrent data-structures do not support snapshots. The snapshot operation allows implementing lock-free, linearizable iterator, size and clear operations - existing concurrent data-structures have implementations which either use global locks or are correct only given that there are no concurrent modifications to the data-structure. In particular, Ctries have an O(1) iterator creation operation, O(1) clear operation, O(1) duplicate operation and an amortized O(logn) size retrieval operation.
Most concurrent data structures require dynamic memory allocation, and lock-free concurrent data structures rely on garbage collection on most platforms. The current implementation [4] of the Ctrie is written for the JVM, where garbage collection is provided by the platform itself. While it's possible to keep a concurrent memory pool for the nodes shared by all instances of Ctries in an application or use reference counting to properly deallocate nodes, the only implementation so far to deal with manual memory management of nodes used in Ctries is the common-lisp implementation cl-ctrie, which implements several stop-and-copy and mark-and-sweep garbage collection techniques for persistent, memory-mapped storage. Hazard pointers are another possible solution for a correct manual management of removed nodes. Such a technique may be viable for managed environments as well, since it could lower the pressure on the GC. A Ctrie implementation in Rust makes use of hazard pointers for this purpose. [6]
A Ctrie implementation [4] for Scala 2.9.x is available on GitHub. It is a mutable thread-safe implementation which ensures progress and supports lock-free, linearizable, O(1) snapshots.
Ctries were first described in 2011 by Aleksandar Prokopec. [1] To quote the author:
Ctrie is a non-blocking concurrent shared-memory hash trie based on single-word compare-and-swap instructions. Insert, lookup and remove operations modifying different parts of the hash trie can be run independent of each other and do not contend. Remove operations ensure that the unneeded memory is freed and that the trie is kept compact.
In 2012, a revised version of the Ctrie data structure was published, [2] simplifying the data structure and introducing an optional constant-time, lock-free, atomic snapshot operation.
In 2018, the closely related Cache-Trie data structure was proposed, [16] which augmented Ctries with an auxiliary, quiescently consistent cache data structure. This "cache" is a hash-table-like entity that makes a best effort to "guess" the appropriate node on a deeper level of the trie, and is maintained in a way such that it's as close as possible to the level where most of the trie's elements are. Cache tries were shown to have amortized expected O(1) complexity of all the basic operations.
In computer science, a data structure is a data organization, management, and storage format that is usually chosen for efficient access to data. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data, i.e., it is an algebraic structure about data.
In computing, a hash table, also known as hash map, is a data structure that implements an associative array or dictionary. It is an abstract data type that maps keys to values. A hash table uses a hash function to compute an index, also called a hash code, into an array of buckets or slots, from which the desired value can be found. During lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored.
In computer science, a priority queue is an abstract data-type similar to a regular queue or stack data structure. Each element in a priority queue has an associated priority. In a priority queue, elements with high priority are served before elements with low priority. In some implementations, if two elements have the same priority, they are served in the same order that they were enqueued in. In other implementations, the order of elements with the same priority is undefined.
In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.
In computing, a persistent data structure or not ephemeral data structure is a data structure that always preserves the previous version of itself when it is modified. Such data structures are effectively immutable, as their operations do not (visibly) update the structure in-place, but instead always yield a new updated structure. The term was introduced in Driscoll, Sarnak, Sleator, and Tarjans' 1986 article.
In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
In concurrent programming, an operation is linearizable if it consists of an ordered list of invocation and response events, that may be extended by adding response events such that:
In computer science, a dynamic array, growable array, resizable array, dynamic table, mutable array, or array list is a random access, variable-size list data structure that allows elements to be added or removed. It is supplied with standard libraries in many modern mainstream programming languages. Dynamic arrays overcome a limit of static arrays, which have a fixed capacity that needs to be specified at allocation.
In computer science, software transactional memory (STM) is a concurrency control mechanism analogous to database transactions for controlling access to shared memory in concurrent computing. It is an alternative to lock-based synchronization. STM is a strategy implemented in software, rather than as a hardware component. A transaction in this context occurs when a piece of code executes a series of reads and writes to shared memory. These reads and writes logically occur at a single instant in time; intermediate states are not visible to other (successful) transactions. The idea of providing hardware support for transactions originated in a 1986 paper by Tom Knight. The idea was popularized by Maurice Herlihy and J. Eliot B. Moss. In 1995 Nir Shavit and Dan Touitou extended this idea to software-only transactional memory (STM). Since 2005, STM has been the focus of intense research and support for practical implementations is growing.
In computer science, a radix tree is a data structure that represents a space-optimized trie in which each node that is the only child is merged with its parent. The result is that the number of children of every internal node is at most the radix r of the radix tree, where r is a positive integer and a power x of 2, having x ≥ 1. Unlike regular trees, edges can be labeled with sequences of elements as well as single elements. This makes radix trees much more efficient for small sets and for sets of strings that share long prefixes.
In computer science, a ternary search tree is a type of trie where nodes are arranged in a manner similar to a binary search tree, but with up to three children rather than the binary tree's limit of two. Like other prefix trees, a ternary search tree can be used as an associative map structure with the ability for incremental string search. However, ternary search trees are more space efficient compared to standard prefix trees, at the cost of speed. Common applications for ternary search trees include spell-checking and auto-completion.
A hash array mapped trie (HAMT) is an implementation of an associative array that combines the characteristics of a hash table and an array mapped trie. It is a refined version of the more general notion of a hash tree.
In computer science, an x-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O(log log M), using O(n log M) space, where n is the number of stored values and M is the maximum value in the domain. The structure was proposed by Dan Willard in 1982, along with the more complicated y-fast trie, as a way to improve the space usage of van Emde Boas trees, while retaining the O(log log M) query time.
In computer science, a hash tree is a persistent data structure that can be used to implement sets and maps, intended to replace hash tables in purely functional programming. In its basic form, a hash tree stores the hashes of its keys, regarded as strings of bits, in a trie, with the actual keys and (optional) values stored at the trie's "final" nodes.
The HAT-trie is a type of radix trie that uses array nodes to collect individual key–value pairs under radix nodes and hash buckets into an associative array. Unlike a simple hash table, HAT-tries store key–value in an ordered collection. The original inventors are Nikolas Askitis and Ranjan Sinha. Askitis & Zobel showed that building and accessing the HAT-trie key/value collection is considerably faster than other sorted access methods and is comparable to the array hash which is an unsorted collection. This is due to the cache-friendly nature of the data structure which attempts to group access to data in time and space into the 64 byte cache line size of the modern CPU.
In computer science, persistent memory is any method or apparatus for efficiently storing data structures such that they can continue to be accessed using memory instructions or memory APIs even after the end of the process that created or last modified them.
A non-blocking linked list is an example of non-blocking data structures designed to implement a linked list in shared memory using synchronization primitives:
In distributed computing, shared-memory systems and message-passing systems are two means of interprocess communication which have been heavily studied. In shared-memory systems, processes communicate by accessing shared data structures. A shared (read/write) register, sometimes just called a register, is a fundamental type of shared data structure which stores a value and has two operations: read, which returns the value stored in the register, and write, which updates the value stored. Other types of shared data structures include read–modify–write, test-and-set, compare-and-swap etc. The memory location which is concurrently accessed is sometimes called a register.
A concurrent hash table or concurrent hash map is an implementation of hash tables allowing concurrent access by multiple threads using a hash function.
The PH-tree is a tree data structure used for spatial indexing of multi-dimensional data (keys) such as geographical coordinates, points, feature vectors, rectangles or bounding boxes. The PH-tree is space partitioning index with a structure similar to that of a quadtree or octree. However, unlike quadtrees, it uses a splitting policy based on tries and similar to Crit bit trees that is based on the bit-representation of the keys. The bit-based splitting policy, when combined with the use of different internal representations for nodes, provides scalability with high-dimensional data. The bit-representation splitting policy also imposes a maximum depth, thus avoiding degenerated trees and the need for rebalancing.