
In computer science, an AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is linear with respect to the height of the tree.

In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. That is, it is a k-ary tree with k = 2. A recursive definition using set theory is that a binary tree is a tuple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set containing the root.
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children. Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as databases and file systems.
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that data access time is linear in respect to the number of nodes in the list. Because nodes are serially linked, accessing any node requires that the prior node be accessed beforehand. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.
In computer science, a red–black tree is a specialised binary search tree data structure noted for fast storage and retrieval of ordered information, and a guarantee that operations will complete within a known time. Compared to other self-balancing binary search trees, the nodes in a red-black tree hold an extra bit called "color" representing "red" and "black" which is used when re-organising the tree to ensure that it is always approximately balanced.

In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children, but must be connected to exactly one parent, except for the root node, which has no parent. These constraints mean there are no cycles or "loops", and also that each child can be treated like the root node of its own subtree, making recursion a useful technique for tree traversal. In contrast to linear data structures, many trees cannot be represented by relationships between neighboring nodes in a single straight line.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.

A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information".
In computer science, tree traversal is a form of graph traversal and refers to the process of visiting each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.

R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons. The R-tree was proposed by Antonin Guttman in 1984 and has found significant use in both theoretical and applied contexts. A common real-world usage for an R-tree might be to store spatial objects such as restaurant locations or the polygons that typical maps are made of: streets, buildings, outlines of lakes, coastlines, etc. and then find answers quickly to queries such as "Find all museums within 2 km of my current location", "retrieve all road segments within 2 km of my location" or "find the nearest gas station". The R-tree can also accelerate nearest neighbor search for various distance metrics, including great-circle distance.
A van Emde Boas tree, also known as a vEB tree or van Emde Boas priority queue, is a tree data structure which implements an associative array with m-bit integer keys. It was invented by a team led by Dutch computer scientist Peter van Emde Boas in 1975. It performs all operations in O(log m) time, or equivalently in time, where is the largest element that can be stored in the tree. The parameter is not to be confused with the actual number of elements stored in the tree, by which the performance of other tree data-structures is often measured.
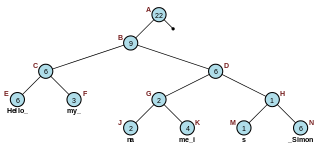
In computer programming, a rope, or cord, is a data structure composed of smaller strings that is used to efficiently store and manipulate a very long string. For example, a text editing program may use a rope to represent the text being edited, so that operations such as insertion, deletion, and random access can be done efficiently.
A B+ tree is an m-ary tree with a variable but often large number of children per node. A B+ tree consists of a root, internal nodes and leaves. The root may be either a leaf or a node with two or more children.
In computer science, a scapegoat tree is a self-balancing binary search tree, invented by Arne Andersson in 1989 and again by Igal Galperin and Ronald L. Rivest in 1993. It provides worst-case lookup time and amortized insertion and deletion time.
An AA tree in computer science is a form of balanced tree used for storing and retrieving ordered data efficiently. AA trees are named after their originator, Swedish computer scientist Arne Andersson.
In computer science, weight-balanced binary trees (WBTs) are a type of self-balancing binary search trees that can be used to implement dynamic sets, dictionaries (maps) and sequences. These trees were introduced by Nievergelt and Reingold in the 1970s as trees of bounded balance, or BB[α] trees. Their more common name is due to Knuth.

In computer science, a queap is a priority queue data structure. The data structure allows insertions and deletions of arbitrary elements, as well as retrieval of the highest-priority element. Each deletion takes amortized time logarithmic in the number of items that have been in the structure for a longer time than the removed item. Insertions take constant amortized time.
In computer science, an x-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O(log log M), using O(n log M) space, where n is the number of stored values and M is the maximum value in the domain. The structure was proposed by Dan Willard in 1982, along with the more complicated y-fast trie, as a way to improve the space usage of van Emde Boas trees, while retaining the O(log log M) query time.
In computer science, a WAVL tree or weak AVL tree is a self-balancing binary search tree. WAVL trees are named after AVL trees, another type of balanced search tree, and are closely related both to AVL trees and red–black trees, which all fall into a common framework of rank balanced trees. Like other balanced binary search trees, WAVL trees can handle insertion, deletion, and search operations in time O(log n) per operation.










