A string-searching algorithm, sometimes called string-matching algorithm, is an algorithm that searches a body of text for portions that match by pattern.
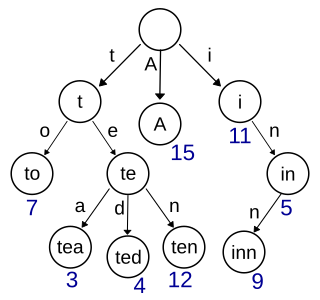
In computer science, a trie, also known as a digital tree or prefix tree, is a specialized search tree data structure used to store and retrieve strings from a dictionary or set. Unlike a binary search tree, nodes in a trie do not store their associated key. Instead, each node's position within the trie determines its associated key, with the connections between nodes defined by individual characters rather than the entire key.
In computer science, the Knuth–Morris–Pratt algorithm is a string-searching algorithm that searches for occurrences of a "word" W within a main "text string" S by employing the observation that when a mismatch occurs, the word itself embodies sufficient information to determine where the next match could begin, thus bypassing re-examination of previously matched characters.
agrep is an open-source approximate string matching program, developed by Udi Manber and Sun Wu between 1988 and 1991, for use with the Unix operating system. It was later ported to OS/2, DOS, and Windows.
In computer science, a mask or bitmask is data that is used for bitwise operations, particularly in a bit field. Using a mask, multiple bits in a byte, nibble, word, etc. can be set either on or off, or inverted from on to off in a single bitwise operation. An additional use of masking involves predication in vector processing, where the bitmask is used to select which element operations in the vector are to be executed and which are not.
In computer science, the Rabin–Karp algorithm or Karp–Rabin algorithm is a string-searching algorithm created by Richard M. Karp and Michael O. Rabin that uses hashing to find an exact match of a pattern string in a text. It uses a rolling hash to quickly filter out positions of the text that cannot match the pattern, and then checks for a match at the remaining positions. Generalizations of the same idea can be used to find more than one match of a single pattern, or to find matches for more than one pattern.
In computer science, the Boyer–Moore string-search algorithm is an efficient string-searching algorithm that is the standard benchmark for practical string-search literature. It was developed by Robert S. Boyer and J Strother Moore in 1977. The original paper contained static tables for computing the pattern shifts without an explanation of how to produce them. The algorithm for producing the tables was published in a follow-on paper; this paper contained errors which were later corrected by Wojciech Rytter in 1980.

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
In computer science, a fusion tree is a type of tree data structure that implements an associative array on w-bit integers on a finite universe, where each of the input integers has size less than 2w and is non-negative. When operating on a collection of n key–value pairs, it uses O(n) space and performs searches in O(logwn) time, which is asymptotically faster than a traditional self-balancing binary search tree, and also better than the van Emde Boas tree for large values of w. It achieves this speed by using certain constant-time operations that can be done on a machine word. Fusion trees were invented in 1990 by Michael Fredman and Dan Willard.
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string, or the digit sum of the binary representation of a given number and the ℓ₁ norm of a bit vector. In this binary case, it is also called the population count, popcount, sideways sum, or bit summation.
In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full-text indices, data-compression algorithms, and the field of bibliometrics.

In combinatorial mathematics, a circular shift is the operation of rearranging the entries in a tuple, either by moving the final entry to the first position, while shifting all other entries to the next position, or by performing the inverse operation. A circular shift is a special kind of cyclic permutation, which in turn is a special kind of permutation. Formally, a circular shift is a permutation σ of the n entries in the tuple such that either
The computer programming languages C and Pascal have similar times of origin, influences, and purposes. Both were used to design their own compilers early in their lifetimes. The original Pascal definition appeared in 1969 and a first compiler in 1970. The first version of C appeared in 1972.
A bit field is a data structure that maps to one or more adjacent bits which have been allocated for specific purposes, so that any single bit or group of bits within the structure can be set or inspected. A bit field is most commonly used to represent integral types of known, fixed bit-width, such as single-bit Booleans.
A BK-tree is a metric tree suggested by Walter Austin Burkhard and Robert M. Keller specifically adapted to discrete metric spaces. For simplicity, consider integer discrete metric . Then, BK-tree is defined in the following way. An arbitrary element a is selected as root node. The root node may have zero or more subtrees. The k-th subtree is recursively built of all elements b such that . BK-trees can be used for approximate string matching in a dictionary.

In computer science, approximate string matching is the technique of finding strings that match a pattern approximately. The problem of approximate string matching is typically divided into two sub-problems: finding approximate substring matches inside a given string and finding dictionary strings that match the pattern approximately.
In computer science and the study of combinatorics on words, a partial word is a string that may contain a number of "do not know" or "do not care" symbols i.e. placeholders in the string where the symbol value is not known or not specified. More formally, a partial word is a partial function where is some finite alphabet. If u(k) is not defined for some then the unknown element at place k in the string is called a "hole". In regular expressions (following the POSIX standard) a hole is represented by the metacharacter ".". For example, aab.ab.b is a partial word of length 8 over the alphabet A ={a,b} in which the fourth and seventh characters are holes.
In computer science, a compressed suffix array is a compressed data structure for pattern matching. Compressed suffix arrays are a general class of data structure that improve on the suffix array. These data structures enable quick search for an arbitrary string with a comparatively small index.
In the C programming language, operations can be performed on a bit level using bitwise operators.
Jewels of Stringology: Text Algorithms is a book on algorithms for pattern matching in strings and related problems. It was written by Maxime Crochemore and Wojciech Rytter, and published by World Scientific in 2003.