Related Research Articles
In computer science, string-searching algorithms, sometimes called string-matching algorithms, are an important class of string algorithms that try to find a place where one or several strings are found within a larger string or text.
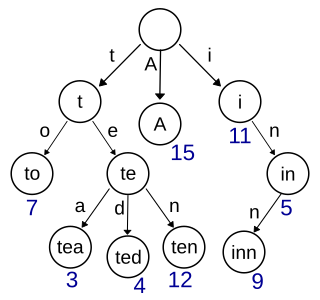
In computer science, a trie, also called digital tree or prefix tree, is a type of search tree: specifically, a k-ary tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.

In computer science, the Aho–Corasick algorithm is a string-searching algorithm invented by Alfred V. Aho and Margaret J. Corasick in 1975. It is a kind of dictionary-matching algorithm that locates elements of a finite set of strings within an input text. It matches all strings simultaneously. The complexity of the algorithm is linear in the length of the strings plus the length of the searched text plus the number of output matches. Note that because all matches are found, multiple matches will be returned for one string location if multiple substrings matched.
In computer science, the Knuth–Morris–Pratt algorithm is a string-searching algorithm that searches for occurrences of a "word" W within a main "text string" S by employing the observation that when a mismatch occurs, the word itself embodies sufficient information to determine where the next match could begin, thus bypassing re-examination of previously matched characters.
In computer science, the Boyer–Moore string-search algorithm is an efficient string-searching algorithm that is the standard benchmark for practical string-search literature. It was developed by Robert S. Boyer and J Strother Moore in 1977. The original paper contained static tables for computing the pattern shifts without an explanation of how to produce them. The algorithm for producing the tables was published in a follow-on paper; this paper contained errors which were later corrected by Wojciech Rytter in 1980.

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full-text indices, data-compression algorithms, and the field of bibliometrics.
The bitap algorithm is an approximate string matching algorithm. The algorithm tells whether a given text contains a substring which is "approximately equal" to a given pattern, where approximate equality is defined in terms of Levenshtein distance – if the substring and pattern are within a given distance k of each other, then the algorithm considers them equal. The algorithm begins by precomputing a set of bitmasks containing one bit for each element of the pattern. Then it is able to do most of the work with bitwise operations, which are extremely fast.

In formal language theory and computer science, a substring is a contiguous sequence of characters within a string. For instance, "the best of" is a substring of "It was the best of times". In contrast, "Itwastimes" is a subsequence of "It was the best of times", but not a substring.

In computer science, approximate string matching is the technique of finding strings that match a pattern approximately. The problem of approximate string matching is typically divided into two sub-problems: finding approximate substring matches inside a given string and finding dictionary strings that match the pattern approximately.

In computer science, a deterministic acyclic finite state automaton (DAFSA), is a data structure that represents a set of strings, and allows for a query operation that tests whether a given string belongs to the set in time proportional to its length. Algorithms exist to construct and maintain such automata, while keeping them minimal. DAFSA is the rediscovery of a data structure called Directed Acyclic Word Graph (DAWG), although the same name had already been given to a different data structure which is related to suffix automaton.
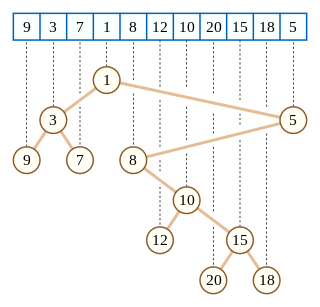
In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.
In computer science, an FM-index is a compressed full-text substring index based on the Burrows–Wheeler transform, with some similarities to the suffix array. It was created by Paolo Ferragina and Giovanni Manzini, who describe it as an opportunistic data structure as it allows compression of the input text while still permitting fast substring queries. The name stands for Full-text index in Minute space.
The term compressed data structure arises in the computer science subfields of algorithms, data structures, and theoretical computer science. It refers to a data structure whose operations are roughly as fast as those of a conventional data structure for the problem, but whose size can be substantially smaller. The size of the compressed data structure is typically highly dependent upon the information entropy of the data being represented.
In computer science, a compressed suffix array is a compressed data structure for pattern matching. Compressed suffix arrays are a general class of data structure that improve on the suffix array. These data structures enable quick search for an arbitrary string with a comparatively small index.
A factor oracle is a finite state automaton that can efficiently search for factors (substrings) in a body of text. Older techniques, such as suffix trees, were time-efficient but required significant amounts of memory. Factor oracles, by contrast, can be constructed in linear time and space in an incremental fashion.
In computer science, the longest common prefix array is an auxiliary data structure to the suffix array. It stores the lengths of the longest common prefixes (LCPs) between all pairs of consecutive suffixes in a sorted suffix array.

In computer science, a suffix automaton is an efficient data structure for representing the substring index of a given string which allows the storage, processing, and retrieval of compressed information about all its substrings. The suffix automaton of a string is the smallest directed acyclic graph with a dedicated initial vertex and a set of "final" vertices, such that paths from the initial vertex to final vertices represent the suffixes of the string.

Gad Menahem Landau is an Israeli computer scientist noted for his contributions to combinatorial pattern matching and string algorithms and is the founding department chair of the Computer Science Department at the University of Haifa.
References
- 1 2 3 4 Barsky, Marina; Stege, Ulrike; Thomo, Alex (2012), "Chapter 1: Structures for Indexing Substrings", Full-Text (Substring) Indexes in External Memory, Synthesis Lectures on Data Management, Springer International Publishing, pp. 1–15, doi:10.1007/978-3-031-01885-5_1, ISBN 9783031018855
- ↑ Risvik, Knut Magne (1998), "Approximate word sequence matching over sparse suffix trees", in Farach-Colton, Martin (ed.), Combinatorial Pattern Matching, 9th Annual Symposium, CPM 98, Piscataway, New Jersey, USA, July 20–22, 1998, Proceedings, Lecture Notes in Computer Science, vol. 1448, Springer, pp. 65–79, doi:10.1007/BFB0030781
- 1 2 3 Grossi, Roberto; Vitter, Jeffrey Scott (2005), "Compressed suffix arrays and suffix trees with applications to text indexing and string matching" (PDF), SIAM Journal on Computing, 35 (2): 378–407, doi:10.1137/S0097539702402354, MR 2191449
- ↑ Blumer, Anselm; Blumer, J.; Ehrenfeucht, Andrzej; Haussler, David; McConnell, Ross M. (1984), "Building the minimal DFA for the set of all subwords of a word on-line in linear time", in Paredaens, Jan (ed.), Automata, Languages and Programming, 11th Colloquium, Antwerp, Belgium, July 16–20, 1984, Proceedings, Lecture Notes in Computer Science, vol. 172, Springer, pp. 109–118, doi:10.1007/3-540-13345-3_9
- ↑ Manber, Udi; Myers, Gene (1993), "Suffix arrays: a new method for on-line string searches", SIAM Journal on Computing , 22 (5): 935–948, doi:10.1137/0222058, MR 1237156
- ↑ Ferragina, Paolo; Manzini, Giovanni (2005), "Indexing compressed text", Journal of the ACM , 52 (4): 552–581, doi:10.1145/1082036.1082039, MR 2164632