In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.
In general relativity, Eddington–Finkelstein coordinates are a pair of coordinate systems for a Schwarzschild geometry which are adapted to radial null geodesics. Null geodesics are the worldlines of photons; radial ones are those that are moving directly towards or away from the central mass. They are named for Arthur Stanley Eddington and David Finkelstein. Although they appear to have inspired the idea, neither ever wrote down these coordinates or the metric in these coordinates. Roger Penrose seems to have been the first to write down the null form but credits it to the above paper by Finkelstein, and, in his Adams Prize essay later that year, to Eddington and Finkelstein. Most influentially, Misner, Thorne and Wheeler, in their book Gravitation, refer to the null coordinates by that name.

In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called canonical transformations, which map canonical coordinate systems into canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself as one of the new canonical momentum coordinates.
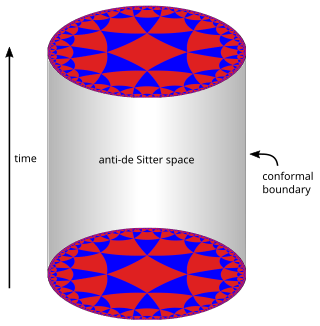
In mathematics and physics, n-dimensional anti-de Sitter space (AdSn) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Paul Dirac was the first person to rigorously explore anti-de Sitter space, doing so in 1963.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.
In mathematics, the Fubini–Study metric is a Kähler metric on a complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study.
A theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the Earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori. This provides a means to inform and verify the formalism.
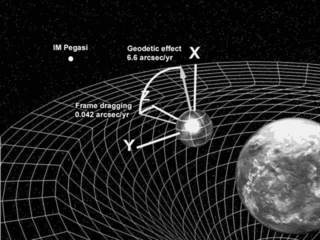
The geodetic effect represents the effect of the curvature of spacetime, predicted by general relativity, on a vector carried along with an orbiting body. For example, the vector could be the angular momentum of a gyroscope orbiting the Earth, as carried out by the Gravity Probe B experiment. The geodetic effect was first predicted by Willem de Sitter in 1916, who provided relativistic corrections to the Earth–Moon system's motion. De Sitter's work was extended in 1918 by Jan Schouten and in 1920 by Adriaan Fokker. It can also be applied to a particular secular precession of astronomical orbits, equivalent to the rotation of the Laplace–Runge–Lenz vector.
In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space. It is named after French mathematician Jean Gaston Darboux.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric.
In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form. These concepts were put in their current form with principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.
A synchronous frame is a reference frame in which the time coordinate defines proper time for all co-moving observers. It is built by choosing some constant time hypersurface as an origin, such that has in every point a normal along the time line and a light cone with an apex in that point can be constructed; all interval elements on this hypersurface are space-like. A family of geodesics normal to this hypersurface are drawn and defined as the time coordinates with a beginning at the hypersurface. In terms of metric-tensor components , a synchronous frame is defined such that

In mathematics, a Cayley–Klein metric is a metric on the complement of a fixed quadric in a projective space which is defined using a cross-ratio. The construction originated with Arthur Cayley's essay "On the theory of distance" where he calls the quadric the absolute. The construction was developed in further detail by Felix Klein in papers in 1871 and 1873, and subsequent books and papers. The Cayley–Klein metrics are a unifying idea in geometry since the method is used to provide metrics in hyperbolic geometry, elliptic geometry, and Euclidean geometry. The field of non-Euclidean geometry rests largely on the footing provided by Cayley–Klein metrics.

The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an oblate ellipsoid, a slightly flattened sphere. A geodesic is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry.
Calculations in the Newman–Penrose (NP) formalism of general relativity normally begin with the construction of a complex null tetrad, where is a pair of real null vectors and is a pair of complex null vectors. These tetrad vectors respect the following normalization and metric conditions assuming the spacetime signature
Spherical wave transformations leave the form of spherical waves as well as the laws of optics and electrodynamics invariant in all inertial frames. They were defined between 1908 and 1909 by Harry Bateman and Ebenezer Cunningham, with Bateman giving the transformation its name. They correspond to the conformal group of "transformations by reciprocal radii" in relation to the framework of Lie sphere geometry, which were already known in the 19th century. Time is used as fourth dimension as in Minkowski space, so spherical wave transformations are connected to the Lorentz transformation of special relativity, and it turns out that the conformal group of spacetime includes the Lorentz group and the Poincaré group as subgroups. However, only the Lorentz/Poincaré groups represent symmetries of all laws of nature including mechanics, whereas the conformal group is related to certain areas such as electrodynamics. In addition, it can be shown that the conformal group of the plane is isomorphic to the Lorentz group.

Isentropic expansion waves are created when a supersonic flow is redirected along a curved surface. These waves are studied to obtain a relation between deflection angle and Mach number. Each wave in this case is a Mach wave, so it is at an angle , where M is the Mach number immediately before the wave. Expansion waves are divergent because as the flow expands the value of Mach number increases, thereby decreasing the Mach angle.
In mathematics Abel elliptic functions are a special kind of elliptic functions, that were established by the Norwegian mathematician Niels Henrik Abel. He published his paper "Recherches sur les Fonctions elliptiques" in Crelle's Journal in 1827. It was the first work on elliptic functions that was actually published. Abel's work on elliptic functions also influenced Jacobi's studies of elliptic functions, whose 1829 published book "Fundamenta nova theoriae functionum ellipticarum" became the standard work on elliptic functions.
In differential geometry, a branch of mathematics, the Moser's trick is a method to relate two differential forms and on a smooth manifold by a diffeomorphism such that , provided that one can find a family of vector fields satisfying a certain ODE.





















