This is a list of potential energy functions that are frequently used in quantum mechanics and have any meaning.

Diatomic molecules are molecules composed of only two atoms, of the same or different chemical elements. If a diatomic molecule consists of two atoms of the same element, such as hydrogen or oxygen, then it is said to be homonuclear. Otherwise, if a diatomic molecule consists of two different atoms, such as carbon monoxide or nitric oxide, the molecule is said to be heteronuclear. The bond in a homonuclear diatomic molecule is non-polar.

Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms.

In nuclear physics, atomic physics, and nuclear chemistry, the nuclear shell model utilizes the Pauli exclusion principle to model the structure of atomic nuclei in terms of energy levels. The first shell model was proposed by Dmitri Ivanenko in 1932. The model was developed in 1949 following independent work by several physicists, most notably Maria Goeppert Mayer and J. Hans D. Jensen, who received the 1963 Nobel Prize in Physics for their contributions to this model, and Eugene Wigner, who received the Nobel Prize alongside them for his earlier groundlaying work on the atomic nuclei.

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle in physics, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves.

A quantum well is a potential well with only discrete energy values.

The Morse potential, named after physicist Philip M. Morse, is a convenient interatomic interaction model for the potential energy of a diatomic molecule. It is a better approximation for the vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond breaking, such as the existence of unbound states. It also accounts for the anharmonicity of real bonds and the non-zero transition probability for overtone and combination bands. The Morse potential can also be used to model other interactions such as the interaction between an atom and a surface. Due to its simplicity, it is not used in modern spectroscopy. However, its mathematical form inspired the MLR (Morse/Long-range) potential, which is the most popular potential energy function used for fitting spectroscopic data.
In theoretical physics, supersymmetric quantum mechanics is an area of research where supersymmetry are applied to the simpler setting of plain quantum mechanics, rather than quantum field theory. Supersymmetric quantum mechanics has found applications outside of high-energy physics, such as providing new methods to solve quantum mechanical problems, providing useful extensions to the WKB approximation, and statistical mechanics.
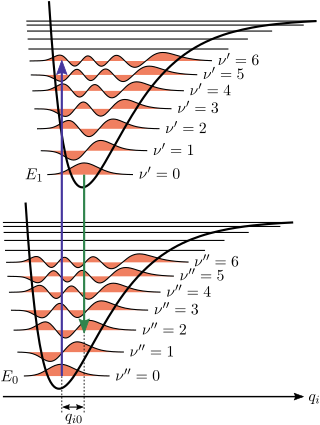
The Franck-Condon Principle describes the intensities of vibronic transitions, or the absorption or emission of a photon. It states that when a molecule is undergoing an electronic transition, such as ionization, the nuclear configuration of the molecule experiences no significant change.

In classical mechanics, anharmonicity is the deviation of a system from being a harmonic oscillator. An oscillator that is not oscillating in harmonic motion is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be calculated using perturbation theory. If the anharmonicity is large, then other numerical techniques have to be used. In reality all oscillating systems are anharmonic, but most approximate the harmonic oscillator the smaller the amplitude of the oscillation is.
In quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it corresponds to a potential which is zero everywhere, except at a single point, where it takes an infinite value. This can be used to simulate situations where a particle is free to move in two regions of space with a barrier between the two regions. For example, an electron can move almost freely in a conducting material, but if two conducting surfaces are put close together, the interface between them acts as a barrier for the electron that can be approximated by a delta potential.
A resonant-tunneling diode (RTD) is a diode with a resonant-tunneling structure in which electrons can tunnel through some resonant states at certain energy levels. The current–voltage characteristic often exhibits negative differential resistance regions.
A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies range from less than 1013 Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 μm.
Quantum dissipation is the branch of physics that studies the quantum analogues of the process of irreversible loss of energy observed at the classical level. Its main purpose is to derive the laws of classical dissipation from the framework of quantum mechanics. It shares many features with the subjects of quantum decoherence and quantum theory of measurement.
In mathematical physics, a Pöschl–Teller potential, named after the physicists Herta Pöschl and Edward Teller, is a special class of potentials for which the one-dimensional Schrödinger equation can be solved in terms of special functions.
In vibrational spectroscopy, an overtone band is the spectral band that occurs in a vibrational spectrum of a molecule when the molecule makes a transition from the ground state (v=0) to the second excited state (v=2), where v is the vibrational quantum number obtained from solving the Schrödinger equation for the molecule.
The trigonometric Rosen–Morse potential, named after the physicists Nathan Rosen and Philip M. Morse, is among the exactly solvable quantum mechanical potentials.
The Nilsson model is a nuclear shell model treating the atomic nucleus as a deformed sphere. In 1953, the first experimental examples were found of rotational bands in nuclei, with their energy levels following the same J(J+1) pattern of energies as in rotating molecules. Quantum mechanically, it is impossible to have a collective rotation of a sphere, so this implied that the shape of these nuclei was nonspherical. In principle, these rotational states could have been described as coherent superpositions of particle-hole excitations in the basis consisting of single-particle states of the spherical potential. But in reality, the description of these states in this manner is intractable, due to the large number of valence particles—and this intractability was even greater in the 1950s, when computing power was extremely rudimentary. For these reasons, Aage Bohr, Ben Mottelson, and Sven Gösta Nilsson constructed models in which the potential was deformed into an ellipsoidal shape. The first successful model of this type is the one now known as the Nilsson model. It is essentially a nuclear shell model using a harmonic oscillator potential, but with anisotropy added, so that the oscillator frequencies along the three Cartesian axes are not all the same. Typically the shape is a prolate ellipsoid, with the axis of symmetry taken to be z.