Map graph

Last updated December 22, 2024

The Four Corners of the USA. Even though these four states meet at a point, rather than sharing a boundary of nonzero length, they form adjacent vertices in the corresponding map graph.

The king's graph, the map graph of squares of the chessboard. A chess king can move between any two adjacent vertices of this graph.

In graph theory, a branch of mathematics, a map graph is an undirected graph formed as the intersection graph of finitely many simply connected and internally disjoint regions of the Euclidean plane. The map graphs include the planar graphs, but are more general. Any number of regions can meet at a common corner (as in the Four Corners of the United States, where four states meet), and when they do the map graph will contain a clique connecting the corresponding vertices, unlike planar graphs in which the largest cliques have only four vertices.^[1] Another example of a map graph is the king's graph, a map graph of the squares of the chessboard connecting pairs of squares between which the chess king can move.

Combinatorial representation

Map graphs can be represented combinatorially as the "half-squares of planar bipartite graphs". That is, let $G = (U, V, E)$ be a planar bipartite graph, with bipartition $(U, V)$ . The square of $G$ is another graph on the same vertex set, in which two vertices are adjacent in the square when they are at most two steps apart in $G$ . The half-square or bipartite half is the induced subgraph of one side of the bipartition (say $V$ ) in the square graph: its vertex set is $V$ and it has an edge between each two vertices in $V$ that are two steps apart in $G$ . The half-square is a map graph. It can be represented geometrically by finding a planar embedding of $G$ , and expanding each vertex of $V$ and its adjacent edges into a star-shaped region, so that these regions touch at the vertices of $U$ . Conversely, every map graph can be represented as a half-square in this way.^[1]

Computational complexity

In 1998, Mikkel Thorup claimed that map graphs can be recognized in polynomial time.^[2] However, the high exponent of the algorithm that he sketched makes it impractical, and Thorup has not published the details of his method and its proof.^[3]

The maximum independent set problem has a polynomial-time approximation scheme for map graphs, and the chromatic number can be approximated to within a factor of two in polynomial time.^[4] The theory of bidimensionality leads to many other approximation algorithms and fixed-parameter tractable algorithms for optimization problems on map graphs.^[5]^[6]^[7]

Variations and related concepts

A $k$ -map graph is a map graph derived from a set of regions in which at most $k$ regions meet at any point. Equivalently, it is the half-square of a planar bipartite graph in which the vertex set $U$ (the side of the bipartition not used to induce the half-square) has maximum degree $k$ . A 3-map graph is a planar graph, and every planar graph can be represented as a 3-map graph. Every 4-map graph is a 1-planar graph, a graph that can be drawn with at most one crossing per edge, and every optimal 1-planar graph (a graph formed from a planar quadrangulation by adding two crossing diagonals to every quadrilateral face) is a 4-map graph. However, some other 1-planar graphs are not map graphs, because (unlike map graphs) their 1-planar drawings include crossing edges that are not part of a four-vertex complete subgraph. As an example, the utility graph $K_{3,3}$ is 1-planar, but has no four-vertex complete subgraph, so it is not a 4-map graph.^[1]

Related Research Articles

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph, or a planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In computer science, the clique problem is the computational problem of finding cliques in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique, finding a maximum weight clique in a weighted graph, listing all maximal cliques, and solving the decision problem of testing whether a graph contains a clique larger than a given size.

In graph theory, an undirected graph $H$ is called a minor of the graph $G$ if $H$ can be formed from $G$ by deleting edges, vertices and by contracting edges.

In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set $of vertices such that for every two vertices in, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening.$

In graph theory, a vertex cover of a graph is a set of vertices that includes at least one endpoint of every edge of the graph.

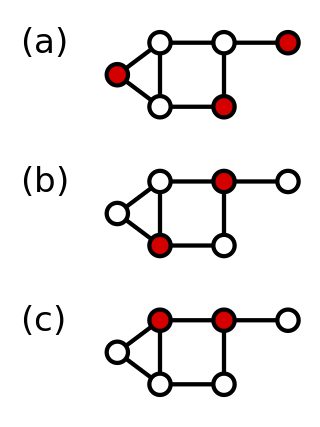
<span class="mw-page-title-main">Dominating set</span> Subset of a graphs nodes such that all other nodes link to at least one

In graph theory, a dominating set for a graph $G$ is a subset $D$ of its vertices, such that any vertex of $G$ is in $D$ , or has a neighbor in $D$ . The domination number $γ(G)$ is the number of vertices in a smallest dominating set for $G$ .

In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at least one edge out of every cycle in the graph. Removing these edges from the graph breaks all of the cycles, producing an acyclic subgraph of the given graph, often called a directed acyclic graph. A feedback arc set with the fewest possible edges is a minimum feedback arc set and its removal leaves a maximum acyclic subgraph; weighted versions of these optimization problems are also used. If a feedback arc set is minimal, meaning that removing any edge from it produces a subset that is not a feedback arc set, then it has an additional property: reversing all of its edges, rather than removing them, produces a directed acyclic graph.

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. An example of graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly $k$ are called $k$ -trees, and the graphs with treewidth at most $k$ are called partial $k$ -trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a path decomposition of a graph $G$ is, informally, a representation of $G$ as a "thickened" path graph, and the pathwidth of $G$ is a number that measures how much the path was thickened to form $G$ . More formally, a path-decomposition is a sequence of subsets of vertices of $G$ such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

In graph theory, the clique-width of a graph $G$ is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct $G$ by means of the following 4 operations :

Creation of a new vertex $v$ with label $i$ (denoted by $i (v)$ )
Disjoint union of two labeled graphs $G$ and $H$ (denoted by $)$
Joining by an edge every vertex labeled $i$ to every vertex labeled $j$ (denoted by $η (i, j)$ ), where $i \neq j$
Renaming label $i$ to label $j$ (denoted by $ρ (i, j)$ )

In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of ⁠ $⁠$ vertices from an $n$ -vertex graph can partition the graph into disjoint subgraphs each of which has at most ⁠ $⁠$ vertices.

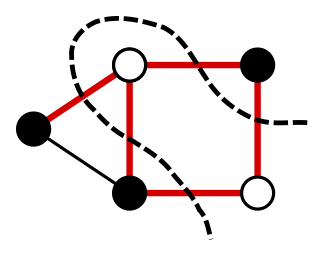
<span class="mw-page-title-main">Maximum cut</span> Problem of finding a maximum cut in a graph

In a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets $S$ and $T$ , such that the number of edges between $S$ and $T$ is as large as possible. Finding such a cut is known as the max-cut problem.

Bidimensionality theory characterizes a broad range of graph problems (bidimensional) that admit efficient approximate, fixed-parameter or kernel solutions in a broad range of graphs. These graph classes include planar graphs, map graphs, bounded-genus graphs and graphs excluding any fixed minor. In particular, bidimensionality theory builds on the graph minor theory of Robertson and Seymour by extending the mathematical results and building new algorithmic tools. The theory was introduced in the work of Demaine, Fomin, Hajiaghayi, and Thilikos, for which the authors received the Nerode Prize in 2015.

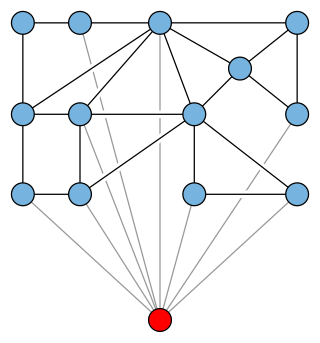
In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. It is an apex, not the apex because an apex graph may have more than one apex; for example, in the minimal nonplanar graphs $K 5$ or $K 3,3$ , every vertex is an apex. The apex graphs include graphs that are themselves planar, in which case again every vertex is an apex. The null graph is also counted as an apex graph even though it has no vertex to remove.

In graph theory and computer science, a dense subgraph is a subgraph with many edges per vertex. This is formalized as follows: let $G = (V, E)$ be an undirected graph and let $S = (V S, E S)$ be a subgraph of $G$ . Then the density of $S$ is defined to be:

In theoretical computer science, Baker's technique is a method for designing polynomial-time approximation schemes (PTASs) for problems on planar graphs. It is named after Brenda Baker, who announced it in a 1983 conference and published it in the Journal of the ACM in 1994.

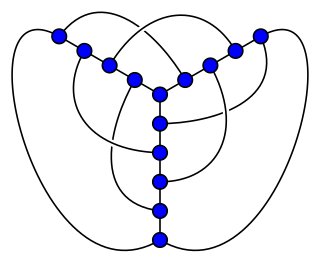
In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge. If a 1-planar graph, one of the most natural generalizations of planar graphs, is drawn that way, the drawing is called a 1-plane graph or 1-planar embedding of the graph.

In graph theory, a branch of mathematics, Halin's grid theorem states that the infinite graphs with thick ends are exactly the graphs containing subdivisions of the hexagonal tiling of the plane. It was published by Rudolf Halin, and is a precursor to the work of Robertson and Seymour linking treewidth to large grid minors, which became an important component of the algorithmic theory of bidimensionality.

<span class="mw-page-title-main">Bipartite half</span> Graph whose nodes are one of the vertex sets of a bipartite graph

In graph theory, the bipartite half or half-square of a bipartite graph $G = (U, V, E)$ is a graph whose vertex set is one of the two sides of the bipartition (without loss of generality, $U$ ) and in which there is an edge $u i u j$ for each pair of vertices $u i, u j$ in $U$ that are at distance two from each other in $G$ . That is, in a more compact notation, the bipartite half is $G 2 [U]$ where the superscript 2 denotes the square of a graph and the square brackets denote an induced subgraph.

In graph theory, an odd cycle transversal of an undirected graph is a set of vertices of the graph that has a nonempty intersection with every odd cycle in the graph. Removing the vertices of an odd cycle transversal from a graph leaves a bipartite graph as the remaining induced subgraph.

References

1 2 3 Chen, Zhi-Zhong; Grigni, Michelangelo; Papadimitriou, Christos H. (2002), "Map graphs", Journal of the ACM , 49 (2): 127–138, arXiv: cs/9910013 , doi:10.1145/506147.506148, MR 2147819, S2CID 2657838 .
↑ Thorup, Mikkel (1998), "Map graphs in polynomial time", Proceedings of the 39th Annual Symposium on Foundations of Computer Science (FOCS 1998), pp. 396–405, doi:10.1109/SFCS.1998.743490, ISBN 978-0-8186-9172-0, S2CID 36845908 .
↑ Brandenburg, Franz J. (August 2018), "Characterizing and Recognizing 4-Map Graphs", Algorithmica , 81 (5): 1818–1843, doi:10.1007/s00453-018-0510-x, S2CID 254038620
↑ Chen, Zhi-Zhong (2001), "Approximation algorithms for independent sets in map graphs", Journal of Algorithms, 41 (1): 20–40, doi:10.1006/jagm.2001.1178, MR 1855346 .
↑ Demaine, Erik D.; Fomin, Fedor V.; Hajiaghayi, Mohammadtaghi; Thilikos, Dimitrios M. (2005), "Fixed-parameter algorithms for $(k, r)$ -center in planar graphs and map graphs", ACM Transactions on Algorithms, 1 (1): 33–47, CiteSeerX 10.1.1.113.2070 , doi:10.1145/1077464.1077468, MR 2163129, S2CID 2757196 .
↑ Demaine, Erik D.; Hajiaghayi, Mohammadtaghi (2007), "The Bidimensionality Theory and Its Algorithmic Applications", The Computer Journal, 51 (3): 292–302, doi:10.1093/comjnl/bxm033, hdl: 1721.1/33090 .
↑ Fomin, Fedor V.; Lokshtanov, Daniel; Saurabh, Saket (2012), "Bidimensionality and geometric graphs", Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2012), pp. 1563–1575, arXiv: 1107.2221 , doi:10.1137/1.9781611973099.124, ISBN 978-1-61197-210-8, MR 3205314, S2CID 9336216 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[cgp-1] 1 2 3 Chen, Zhi-Zhong; Grigni, Michelangelo; Papadimitriou, Christos H. (2002), "Map graphs", Journal of the ACM , 49 (2): 127–138, arXiv: cs/9910013 , doi:10.1145/506147.506148, MR 2147819, S2CID 2657838 .

[2] Thorup, Mikkel (1998), "Map graphs in polynomial time", Proceedings of the 39th Annual Symposium on Foundations of Computer Science (FOCS 1998), pp. 396–405, doi:10.1109/SFCS.1998.743490, ISBN 978-0-8186-9172-0, S2CID 36845908 .

[3] Brandenburg, Franz J. (August 2018), "Characterizing and Recognizing 4-Map Graphs", Algorithmica , 81 (5): 1818–1843, doi:10.1007/s00453-018-0510-x, S2CID 254038620

[4] Chen, Zhi-Zhong (2001), "Approximation algorithms for independent sets in map graphs", Journal of Algorithms, 41 (1): 20–40, doi:10.1006/jagm.2001.1178, MR 1855346 .

[5] Demaine, Erik D.; Fomin, Fedor V.; Hajiaghayi, Mohammadtaghi; Thilikos, Dimitrios M. (2005), "Fixed-parameter algorithms for $(k, r)$ -center in planar graphs and map graphs", ACM Transactions on Algorithms, 1 (1): 33–47, CiteSeerX 10.1.1.113.2070 , doi:10.1145/1077464.1077468, MR 2163129, S2CID 2757196 .

[6] Demaine, Erik D.; Hajiaghayi, Mohammadtaghi (2007), "The Bidimensionality Theory and Its Algorithmic Applications", The Computer Journal, 51 (3): 292–302, doi:10.1093/comjnl/bxm033, hdl: 1721.1/33090 .

[7] Fomin, Fedor V.; Lokshtanov, Daniel; Saurabh, Saket (2012), "Bidimensionality and geometric graphs", Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2012), pp. 1563–1575, arXiv: 1107.2221 , doi:10.1137/1.9781611973099.124, ISBN 978-1-61197-210-8, MR 3205314, S2CID 9336216 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]