In graph theory, the bipartite half or half-square of a bipartite graph G = (U,V,E) is a graph whose vertex set is one of the two sides of the bipartition (without loss of generality, U) and in which there is an edge uiuj for each pair of vertices ui, uj in U that are at distance two from each other in G. [1] That is, in a more compact notation, the bipartite half is G2[U] where the superscript 2 denotes the square of a graph and the square brackets denote an induced subgraph.
For instance, the bipartite half of the complete bipartite graph Kn,n is the complete graph Kn and the bipartite half of the hypercube graph is the halved cube graph. When G is a distance-regular graph, its two bipartite halves are both distance-regular. [2] For instance, the halved Foster graph is one of finitely many degree-6 distance-regular locally linear graphs. [3]
Every graph G is the bipartite half of another graph, formed by subdividing the edges of G into two-edge paths. More generally, a representation of G as a bipartite half can be found by taking any clique edge cover of G and replacing each clique by a star. [4] Every representation arises in this way. Since finding the smallest clique edge cover is NP-hard, so is finding the graph with the fewest vertices for which G is the bipartite half. [5]
The map graphs, that is, the intersection graphs of interior-disjoint simply-connected regions in the plane, are exactly the bipartite halves of bipartite planar graphs. [6]
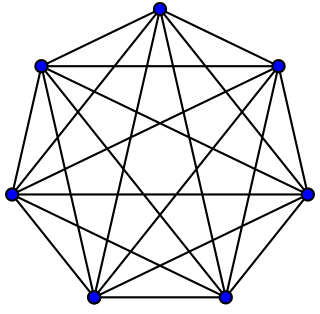
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.
Extremal graph theory is a branch of combinatorics, itself an area of mathematics, that lies at the intersection of extremal combinatorics and graph theory. In essence, extremal graph theory studies how global properties of a graph influence local substructure. Results in extremal graph theory deal with quantitative connections between various graph properties, both global and local, and problems in extremal graph theory can often be formulated as optimization problems: how big or small a parameter of a graph can be, given some constraints that the graph has to satisfy? A graph that is an optimal solution to such an optimization problem is called an extremal graph, and extremal graphs are important objects of study in extremal graph theory.
In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphism
In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.
In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.
In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.
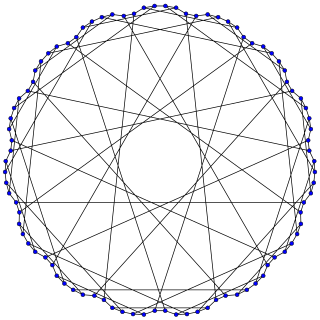
In the mathematical field of graph theory, the Foster graph is a bipartite 3-regular graph with 90 vertices and 135 edges.
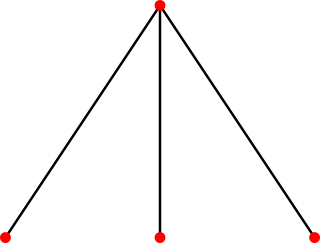
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.
In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.
In graph theory, a well-covered graph is an undirected graph in which the minimal vertex covers all have the same size. Here, a vertex cover is a set of vertices that touches all edges, and it is minimal if removing any vertex from it would leave some edge uncovered. Equivalently, well-covered graphs are the graphs in which all maximal independent sets have equal size. Well-covered graphs were defined and first studied by Michael D. Plummer in 1970.
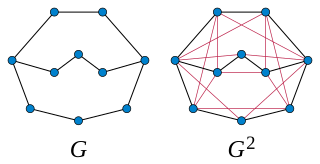
In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.
In graph theory, the halved cube graph or half cube graph of dimension n is the graph of the demihypercube, formed by connecting pairs of vertices at distance exactly two from each other in the hypercube graph. That is, it is the half-square of the hypercube. This connectivity pattern produces two isomorphic graphs, disconnected from each other, each of which is the halved cube graph.
In graph theory, a branch of mathematics, a map graph is an undirected graph formed as the intersection graph of finitely many simply connected and internally disjoint regions of the Euclidean plane. The map graphs include the planar graphs, but are more general. Any number of regions can meet at a common corner, and when they do the map graph will contain a clique connecting the corresponding vertices, unlike planar graphs in which the largest cliques have only four vertices. Another example of a map graph is the king's graph, a map graph of the squares of the chessboard connecting pairs of squares between which the chess king can move.
In graph theory, a branch of mathematics, a half graph is a special type of bipartite graph. These graphs are called the half graphs because they have approximately half of the edges of a complete bipartite graph on the same vertices. The name was given to these graphs by Paul Erdős and András Hajnal.
In graph theory, the Graham–Pollak theorem states that the edges of an -vertex complete graph cannot be partitioned into fewer than complete bipartite graphs. It was first published by Ronald Graham and Henry O. Pollak in two papers in 1971 and 1972, in connection with an application to telephone switching circuitry.
