Related Research Articles
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.

In mathematics, an associative algebra is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.

In mathematics, given two groups, and, a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the ancient Greek language: ὁμός (homos) meaning "same" and μορφή (morphe) meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same". The term "homomorphism" appeared as early as 1892 ; it was attributed to the German mathematician Felix Klein (1849–1925).
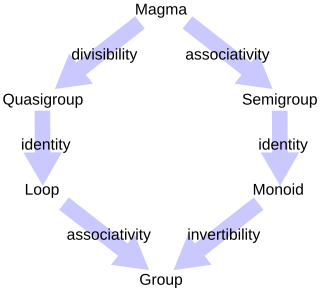
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation.
In algebra, the kernel of a homomorphism is generally the inverse image of 0. An important special case is the kernel of a linear map. The kernel of a matrix, also called the null space, is the kernel of the linear map defined by the matrix.
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams. Turning all arrows around, one obtains the axioms of coalgebras. Every coalgebra, by duality, gives rise to an algebra, but not in general the other way. In finite dimensions, this duality goes in both directions.
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a counital coassociative coalgebra. The algebraic and coalgebraic structures are made compatible with a few more axioms. Specifically, the comultiplication and the counit are both unital algebra homomorphisms, or equivalently, the multiplication and the unit of the algebra both are coalgebra morphisms.
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property. The representation theory of a Hopf algebra is particularly nice, since the existence of compatible comultiplication, counit, and antipode allows for the construction of tensor products of representations, trivial representations, and dual representations.
In mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by S. Bochner (1946). The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between Lie groups and Lie algebras. They are used in algebraic number theory and algebraic topology.
In mathematics, a comodule or corepresentation is a concept dual to a module. The definition of a comodule over a coalgebra is formed by dualizing the definition of a module over an associative algebra.
In mathematics, a pointed set is an ordered pair where is a set and is an element of called the base point, also spelled basepoint.
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite-dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in the 1930s by Brauer and Nesbitt and were named after Frobenius. Nakayama discovered the beginnings of a rich duality theory, . Dieudonné used this to characterize Frobenius algebras. Frobenius algebras were generalized to quasi-Frobenius rings, those Noetherian rings whose right regular representation is injective. In recent times, interest has been renewed in Frobenius algebras due to connections to topological quantum field theory.
In mathematics, the group Hopf algebra of a given group is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices and its algebraic operations. The theory of matrices and linear operators is well-understood, so representations of more abstract objects in terms of familiar linear algebra objects helps glean properties and sometimes simplify calculations on more abstract theories.
In ring theory and Frobenius algebra extensions, areas of mathematics, there is a notion of depth two subring or depth of a Frobenius extension. The notion of depth two is important in a certain noncommutative Galois theory, which generates Hopf algebroids in place of the more classical Galois groups, whereas the notion of depth greater than two measures the defect, or distance, from being depth two in a tower of iterated endomorphism rings above the subring. A more recent definition of depth of any unital subring in any associative ring is proposed in a paper studying the depth of a subgroup of a finite group as group algebras over a commutative ring.
In mathematics, in the theory of Hopf algebras, a Hopf algebroid is a generalisation of weak Hopf algebras, certain skew Hopf algebras and commutative Hopf k-algebroids. If k is a field, a commutative k-algebroid is a cogroupoid object in the category of k-algebras; the category of such is hence dual to the category of groupoid k-schemes. This commutative version has been used in 1970-s in algebraic geometry and stable homotopy theory. The generalization of Hopf algebroids and its main part of the structure, associative bialgebroids, to the noncommutative base algebra was introduced by J.-H. Lu in 1996 as a result on work on groupoids in Poisson geometry. They may be loosely thought of as Hopf algebras over a noncommutative base ring, where weak Hopf algebras become Hopf algebras over a separable algebra. It is a theorem that a Hopf algebroid satisfying a finite projectivity condition over a separable algebra is a weak Hopf algebra, and conversely a weak Hopf algebra H is a Hopf algebroid over its separable subalgebra HL. The antipode axioms have been changed by G. Böhm and K. Szlachányi in 2004 for tensor categorical reasons and to accommodate examples associated to depth two Frobenius algebra extensions.
In mathematics, Moss E. Sweedler introduced an example of an infinite-dimensional Hopf algebra, and Sweedler's Hopf algebraH4 is a certain 4-dimensional quotient of it that is neither commutative nor cocommutative.
Moss Eisenberg Sweedler is an American mathematician, known for Sweedler's Hopf algebra, Sweedler's notation, measuring coalgebras, and his proof, with Harry Prince Allen, of a conjecture of Nathan Jacobson.
In algebra, the Malvenuto–Poirier–Reutenauer Hopf algebra of permutations or MPR Hopf algebra is a Hopf algebra with a basis of all elements of all the finite symmetric groups Sn, and is a non-commutative analogue of the Hopf algebra of symmetric functions. It is both free as an algebra and graded-cofree as a graded coalgebra, so is in some sense as far as possible from being either commutative or cocommutative. It was introduced by Malvenuto & Reutenauer (1994) and studied by Poirier & Reutenauer (1995).
References
- Hazewinkel, Michiel; Gubareni, Nadiya; Kirichenko, V. V. (2010), Algebras, rings and modules. Lie algebras and Hopf algebras, Mathematical Surveys and Monographs, 168, Providence, RI: American Mathematical Society, ISBN 978-0-8218-5262-0, MR 2724822, Zbl 1211.16023
- Sweedler, Moss E. (1968), "The Hopf algebra of an algebra applied to field theory", J. Algebra, 8: 262–276, doi: 10.1016/0021-8693(68)90059-8 , MR 0222053
- Sweedler, Moss E. (1969), Hopf algebras, Mathematics Lecture Note Series, W. A. Benjamin, Inc., New York, MR 0252485, Zbl 0194.32901