
In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

Astronomicalcoordinate systems are organized arrangements for specifying positions of satellites, planets, stars, galaxies, and other celestial objects relative to physical reference points available to a situated observer. Coordinate systems in astronomy can specify an object's position in three-dimensional space or plot merely its direction on a celestial sphere, if the object's distance is unknown or trivial.

In mathematics, a unit vector in a normed vector space is a vector of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in .
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.

In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.

Note: This page uses common physics notation for spherical coordinates, in which is the angle between the z axis and the radius vector connecting the origin to the point in question, while is the angle between the projection of the radius vector onto the x-y plane and the x axis. Several other definitions are in use, and so care must be taken in comparing different sources.

In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.

In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime. A torus knot is trivial if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers , or a subset of that contains an interval of positive length. Most real functions that are considered and studied are differentiable in some interval. The most widely considered such functions are the real functions, which are the real-valued functions of a real variable, that is, the functions of a real variable whose codomain is the set of real numbers.
In statistics, econometrics, and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it is used to describe certain time-varying processes in nature, economics, behavior, etc. The autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term ; thus the model is in the form of a stochastic difference equation. Together with the moving-average (MA) model, it is a special case and key component of the more general autoregressive–moving-average (ARMA) and autoregressive integrated moving average (ARIMA) models of time series, which have a more complicated stochastic structure; it is also a special case of the vector autoregressive model (VAR), which consists of a system of more than one interlocking stochastic difference equation in more than one evolving random variable.
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.
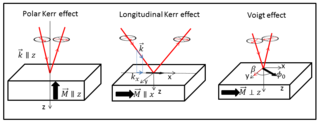
The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are several denominations for this effect in the literature: the Cotton–Mouton effect, the Voigt effect, and magnetic-linear birefringence. This last denomination is closer in the physical sense, where the Voigt effect is a magnetic birefringence of the material with an index of refraction parallel and perpendicular ) to the magnetization vector or to the applied magnetic field.

In mathematics, the dual quaternions are an 8-dimensional real algebra isomorphic to the tensor product of the quaternions and the dual numbers. Thus, they may be constructed in the same way as the quaternions, except using dual numbers instead of real numbers as coefficients. A dual quaternion can be represented in the form A + εB, where A and B are ordinary quaternions and ε is the dual unit, which satisfies ε2 = 0 and commutes with every element of the algebra. Unlike quaternions, the dual quaternions do not form a division algebra.
The Krylov–Bogolyubov averaging method is a mathematical method for approximate analysis of oscillating processes in non-linear mechanics. The method is based on the averaging principle when the exact differential equation of the motion is replaced by its averaged version. The method is named after Nikolay Krylov and Nikolay Bogoliubov.
In mathematical analysis and its applications, a function of several real variables or real multivariate function is a function with more than one argument, with all arguments being real variables. This concept extends the idea of a function of a real variable to several variables. The "input" variables take real values, while the "output", also called the "value of the function", may be real or complex. However, the study of the complex-valued functions may be easily reduced to the study of the real-valued functions, by considering the real and imaginary parts of the complex function; therefore, unless explicitly specified, only real-valued functions will be considered in this article.
The Clohessy–Wiltshire equations describe a simplified model of orbital relative motion, in which the target is in a circular orbit, and the chaser spacecraft is in an elliptical or circular orbit. This model gives a first-order approximation of the chaser's motion in a target-centered coordinate system. It is used to plan the rendezvous of the chaser with the target.

In mathematics, calculus on Euclidean space is a generalization of calculus of functions in one or several variables to calculus of functions on Euclidean space as well as a finite-dimensional real vector space. This calculus is also known as advanced calculus, especially in the United States. It is similar to multivariable calculus but is somehow more sophisticated in that it uses linear algebra more extensively and covers some concepts from differential geometry such as differential forms and Stokes' formula in terms of differential forms. This extensive use of linear algebra also allows a natural generalization of multivariable calculus to calculus on Banach spaces or topological vector spaces.








![Figure 1: Solution to perturbed logistic growth equation
x
.
=
e
(
x
(
1
-
x
)
+
sin
[?]
t
)
x
[?]
R
,
e
=
0.05
{\displaystyle {\dot {x}}=\varepsilon (x(1-x)+\sin {t})~x\in \mathbb {R} ,~\varepsilon =0.05}
(blue solid line) and the averaged equation
y
.
=
e
y
(
1
-
y
)
,
y
[?]
R
{\displaystyle {\dot {y}}=\varepsilon y(1-y),~y\in \mathbb {R} }
(orange solid line). Logistic growth equation.png](http://upload.wikimedia.org/wikipedia/commons/thumb/c/cd/Logistic_growth_equation.png/403px-Logistic_growth_equation.png)






























































![Figure 2: A simple harmonic oscillator with small periodic damping term given by
z
"
+
4
e
cos
2
[?]
(
t
)
z
.
+
z
=
0
,
z
(
0
)
=
0
,
z
.
(
0
)
=
1
;
e
=
0.05
{\displaystyle {\ddot {z}}+4\varepsilon \cos ^{2}{(t)}{\dot {z}}+z=0,~z(0)=0,~{\dot {z}}(0)=1;~\varepsilon =0.05}
.The numerical simulation of the original equation (blue solid line) is compared with averaging system (orange dashed line) and the crude averaged system (green dash-dotted line). The left plot displays the solution evolved in time and the right plot represents on the phase space. We note that the crude averaging disagrees with the expected solution. Averaging example Crude averaging z axis.png](http://upload.wikimedia.org/wikipedia/commons/thumb/6/69/Averaging_example_Crude_averaging_z_axis.png/610px-Averaging_example_Crude_averaging_z_axis.png)






















![Figure 4: The plot depicts two fundamental quantities the average technique is based on: the bounded and connected region
D
{\displaystyle D}
of the phase space and how long (defined by the constant
c
{\displaystyle c}
) the averaged solution is valid. For this case,
z
"
+
z
=
8
e
cos
[?]
(
t
)
z
.
2
,
z
(
0
)
=
0
,
z
.
(
0
)
=
1
;
8
e
=
2
15
{\textstyle {\ddot {z}}+z=8\varepsilon \cos {(t)}{\dot {z}}^{2},~z(0)=0,~{\dot {z}}(0)=1;~8\varepsilon ={\frac {2}{15}}}
. Note that both solutions blow up in finite time. Hence,
D
{\displaystyle D}
has been chosen accordingly in order to maintain the boundedness of the solution and the time interval of validity of the approximation is
0
<=
e
t
<
L
<
1
3
{\displaystyle 0\leq \varepsilon t<L<{\frac {1}{3}}}
. Restricting time scale.png](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e7/Restricting_time_scale.png/462px-Restricting_time_scale.png)







































