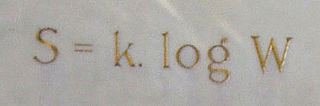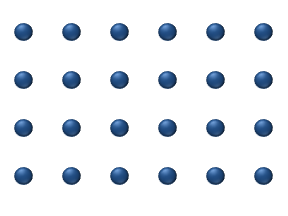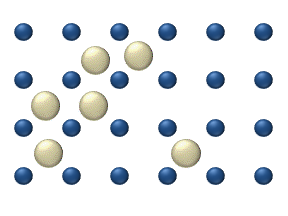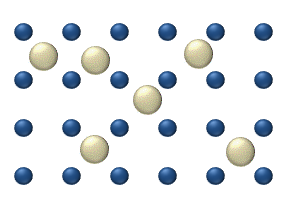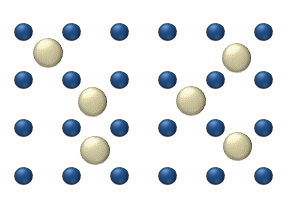In statistical mechanics and mathematics, a Boltzmann distribution is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. The distribution is expressed in the form:

Entropy is a scientific concept that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.

The second law of thermodynamics is a physical law based on universal empirical observation concerning heat and energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter. Another statement is: "Not all heat can be converted into work in a cyclic process."

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as
In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless.
In classical statistical mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency to decrease in the quantity H in a nearly-ideal gas of molecules. As this quantity H was meant to represent the entropy of thermodynamics, the H-theorem was an early demonstration of the power of statistical mechanics as it claimed to derive the second law of thermodynamics—a statement about fundamentally irreversible processes—from reversible microscopic mechanics. It is thought to prove the second law of thermodynamics, albeit under the assumption of low-entropy initial conditions.

The laws of thermodynamics are a set of scientific laws which define a group of physical quantities, such as temperature, energy, and entropy, that characterize thermodynamic systems in thermodynamic equilibrium. The laws also use various parameters for thermodynamic processes, such as thermodynamic work and heat, and establish relationships between them. They state empirical facts that form a basis of precluding the possibility of certain phenomena, such as perpetual motion. In addition to their use in thermodynamics, they are important fundamental laws of physics in general and are applicable in other natural sciences.

Thermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics.
In physics, maximum entropy thermodynamics views equilibrium thermodynamics and statistical mechanics as inference processes. More specifically, MaxEnt applies inference techniques rooted in Shannon information theory, Bayesian probability, and the principle of maximum entropy. These techniques are relevant to any situation requiring prediction from incomplete or insufficient data. MaxEnt thermodynamics began with two papers by Edwin T. Jaynes published in the 1957 Physical Review.
In thermodynamics, the entropy of mixing is the increase in the total entropy when several initially separate systems of different composition, each in a thermodynamic state of internal equilibrium, are mixed without chemical reaction by the thermodynamic operation of removal of impermeable partition(s) between them, followed by a time for establishment of a new thermodynamic state of internal equilibrium in the new unpartitioned closed system.

In statistical mechanics, a microstate is a specific configuration of a system that describes the precise positions and momenta of all the individual particles or components that make up the system. Each microstate has a certain probability of occurring during the course of the system's thermal fluctuations.
The mathematical expressions for thermodynamic entropy in the statistical thermodynamics formulation established by Ludwig Boltzmann and J. Willard Gibbs in the 1870s are similar to the information entropy by Claude Shannon and Ralph Hartley, developed in the 1940s.
The concept of entropy developed in response to the observation that a certain amount of functional energy released from combustion reactions is always lost to dissipation or friction and is thus not transformed into useful work. Early heat-powered engines such as Thomas Savery's (1698), the Newcomen engine (1712) and the Cugnot steam tricycle (1769) were inefficient, converting less than two percent of the input energy into useful work output; a great deal of useful energy was dissipated or lost. Over the next two centuries, physicists investigated this puzzle of lost energy; the result was the concept of entropy.
The concept entropy was first developed by German physicist Rudolf Clausius in the mid-nineteenth century as a thermodynamic property that predicts that certain spontaneous processes are irreversible or impossible. In statistical mechanics, entropy is formulated as a statistical property using probability theory. The statistical entropy perspective was introduced in 1870 by Austrian physicist Ludwig Boltzmann, who established a new field of physics that provided the descriptive linkage between the macroscopic observation of nature and the microscopic view based on the rigorous treatment of large ensembles of microstates that constitute thermodynamic systems.

In thermodynamics, entropy is a numerical quantity that shows that many physical processes can go in only one direction in time. For example, cream and coffee can be mixed together, but cannot be "unmixed"; a piece of wood can be burned, but cannot be "unburned". The word 'entropy' has entered popular usage to refer a lack of order or predictability, or of a gradual decline into disorder. A more physical interpretation of thermodynamic entropy refers to spread of energy or matter, or to extent and diversity of microscopic motion.

Thermodynamic databases contain information about thermodynamic properties for substances, the most important being enthalpy, entropy, and Gibbs free energy. Numerical values of these thermodynamic properties are collected as tables or are calculated from thermodynamic datafiles. Data is expressed as temperature-dependent values for one mole of substance at the standard pressure of 101.325 kPa, or 100 kPa. Both of these definitions for the standard condition for pressure are in use.
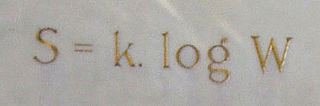
In statistical mechanics, Boltzmann's equation is a probability equation relating the entropy , also written as , of an ideal gas to the multiplicity, the number of real microstates corresponding to the gas's macrostate:

Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measured with a thermometer. It reflects the kinetic energy of the vibrating and colliding atoms making up a substance.
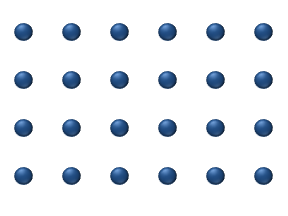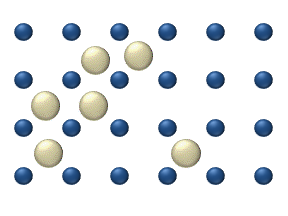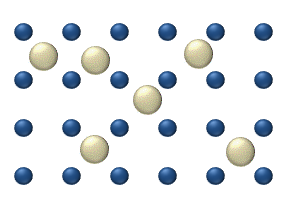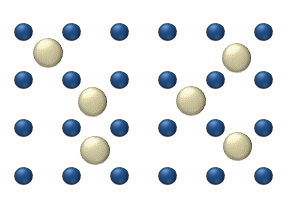
In statistical mechanics, thermal fluctuations are random deviations of an atomic system from its average state, that occur in a system at equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they decrease as temperature approaches absolute zero.