This article needs additional citations for verification .(October 2025) |

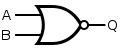
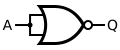
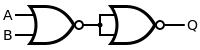
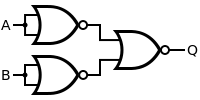
A NOR gate or a NOT OR gate is a logic gate which gives a positive output only when both inputs are negative.
Contents
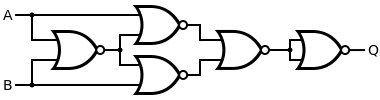
Like NAND gates, NOR gates are so-called "universal gates" that can be combined to form any other kind of logic gate. For example, the first embedded system, the Apollo Guidance Computer, was built exclusively from NOR gates, about 5,600 in total for the later versions. Today, integrated circuits are not constructed exclusively from a single type of gate. Instead, EDA tools are used to convert the description of a logical circuit to a netlist of complex gates (standard cells) or transistors (full custom approach).