| Order-3-6 heptagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {7,3,6} {7,3[3]} |
| Coxeter diagram |       =   |
| Cells | {7,3}  |
| Faces | {7} |
| Vertex figure | {3,6} |
| Dual | {6,3,7} |
| Coxeter group | [7,3,6] [7,3[3]] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-3-6 heptagonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-3-6 heptagonal honeycomb is {7,3,6}, with six heptagonal tilings meeting at each edge. The vertex figure of this honeycomb is a triangular tiling, {3,6}.
It has a quasiregular construction, , which can be seen as alternately colored cells.
 Poincaré disk model |  Ideal surface |
It is a part of a series of regular polytopes and honeycombs with {p,3,6} Schläfli symbol, and triangular tiling vertex figures.
| Form | Paracompact | Noncompact | |||||
|---|---|---|---|---|---|---|---|
| Name | {3,3,6} {3,3[3]} | {4,3,6} {4,3[3]} | {5,3,6} {5,3[3]} | {6,3,6} {6,3[3]} | {7,3,6} {7,3[3]} | {8,3,6} {8,3[3]} | ... {∞,3,6} {∞,3[3]} |
 | |  |  | | |  |  |
| Image |  |  |  |  |  |  |  |
| Cells |  {3,3} |  {4,3} |  {5,3} |  {6,3} |  {7,3} |  {8,3} |  {∞,3} |
| Order-3-6 octagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {8,3,6} {8,3[3]} |
| Coxeter diagram | = |
| Cells | {8,3}  |
| Faces | Octagon {8} |
| Vertex figure | triangular tiling {3,6} |
| Dual | {6,3,8} |
| Coxeter group | [8,3,6] [8,3[3]] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-3-6 octagonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-6 octagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-3-6 octagonal honeycomb is {8,3,6}, with six octagonal tilings meeting at each edge. The vertex figure of this honeycomb is a triangular tiling, {3,6}.
It has a quasiregular construction, , which can be seen as alternately colored cells.
 Poincaré disk model |
| Order-3-6 apeirogonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {∞,3,6} {∞,3[3]} |
| Coxeter diagram | = |
| Cells | {∞,3}  |
| Faces | Apeirogon {∞} |
| Vertex figure | triangular tiling {3,6} |
| Dual | {6,3,∞} |
| Coxeter group | [∞,3,6] [∞,3[3]] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-3-6 apeirogonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-3 apeirogonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-3-6 apeirogonal honeycomb is {∞,3,6}, with six order-3 apeirogonal tilings meeting at each edge. The vertex figure of this honeycomb is a triangular tiling, {3,6}.
 Poincaré disk model |  Ideal surface |
It has a quasiregular construction, , which can be seen as alternately colored cells.
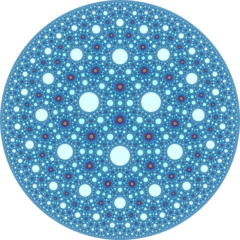
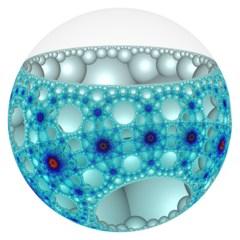
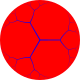
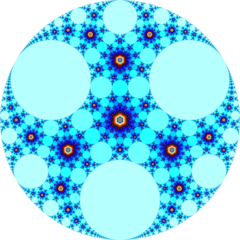
The order-6 cubic honeycomb is a paracompact regular space-filling tessellation in hyperbolic 3-space. It is paracompact because it has vertex figures composed of an infinite number of facets, with all vertices as ideal points at infinity. With Schläfli symbol {4,3,6}, the honeycomb has six ideal cubes meeting along each edge. Its vertex figure is an infinite triangular tiling. Its dual is the order-4 hexagonal tiling honeycomb.
In the field of hyperbolic geometry, the order-6 hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells with an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.
In the geometry of hyperbolic 3-space, the order-7 tetrahedral honeycomb is a regular space-filling tessellation with Schläfli symbol {3,3,7}. It has seven tetrahedra {3,3} around each edge. All vertices are ultra-ideal with infinitely many tetrahedra existing around each vertex in an order-7 triangular tiling vertex arrangement.
In the geometry of hyperbolic 3-space, the order-7 dodecahedral honeycomb is a regular space-filling tessellation.
In the geometry of hyperbolic 3-space, the order-3-7 hexagonal honeycomb or a regular space-filling tessellation with Schläfli symbol {6,3,7}.
In the geometry of hyperbolic 3-space, the heptagonal tiling honeycomb or 7,3,3 honeycomb a regular space-filling tessellation. Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-7 cubic honeycomb is a regular space-filling tessellation. With Schläfli symbol {4,3,7}, it has seven cubes {4,3} around each edge. All vertices are ultra-ideal with infinitely many cubes existing around each vertex in an order-7 triangular tiling vertex arrangement.
In the geometry of hyperbolic 3-space, the order-3-4 heptagonal honeycomb or 7,3,4 honeycomb a regular space-filling tessellation. Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-3-5 heptagonal honeycomb a regular space-filling tessellation. Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-3-7 heptagonal honeycomb a regular space-filling tessellation with Schläfli symbol {7,3,7}.
In the geometry of hyperbolic 3-space, the order-6-4 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,6,4}.
In the geometry of hyperbolic 3-space, the order-4-3 pentagonal honeycomb or 5,4,3 honeycomb is a regular space-filling tessellation. Each infinite cell is an order-4 pentagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-4-4 pentagonal honeycomb a regular space-filling tessellation. Each infinite cell consists of a pentagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-5-3 square honeycomb or 4,5,3 honeycomb a regular space-filling tessellation. Each infinite cell consists of a pentagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-5-4 square honeycomb a regular space-filling tessellation with Schläfli symbol {4,5,4}.
In the geometry of hyperbolic 3-space, the order-7-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,7,3}.
In the geometry of hyperbolic 3-space, the order-6-3 square honeycomb or 4,6,3 honeycomb is a regular space-filling tessellation. Each infinite cell consists of a hexagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
In the geometry of hyperbolic 3-space, the order-6-4 square honeycomb a regular space-filling tessellation with Schläfli symbol {4,6,4}.
In the geometry of hyperbolic 3-space, the order-8-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,8,3}.
In the geometry of hyperbolic 3-space, the order-infinite-3 triangular honeycomb is a regular space-filling tessellation with Schläfli symbol {3,∞,3}.