Related Research Articles

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.
In geometry, a secant is a line that intersects a curve at a minimum of two distinct points. The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant intersects the circle at exactly two points. A chord is the line segment determined by the two points, that is, the interval on the secant whose ends are the two points.
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice versa.

In mathematics, affine geometry is what remains of Euclidean geometry when ignoring the metric notions of distance and angle.
Synthetic geometry is geometry without the use of coordinates. It relies on the axiomatic method for proving all results from a few basic properties initially called postulates, and at present called axioms.

In projective geometry, Desargues's theorem, named after Girard Desargues, states:
In geometry, parallel lines are coplanar infinite straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. Parallel curves are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called skew lines. Line segments and Euclidean vectors are parallel if they have the same direction or opposite direction.
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie as the foundation for a modern treatment of Euclidean geometry. Other well-known modern axiomatizations of Euclidean geometry are those of Alfred Tarski and of George Birkhoff.

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.
In geometry, Pasch's theorem, stated in 1882 by the German mathematician Moritz Pasch, is a result in plane geometry which cannot be derived from Euclid's postulates.

In Euclidean geometry, Menelaus's theorem, named for Menelaus of Alexandria, is a proposition about triangles in plane geometry. Suppose we have a triangle △ABC, and a transversal line that crosses BC, AC, AB at points D, E, F respectively, with D, E, F distinct from A, B, C. A weak version of the theorem states that
In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An incidence structure is what is obtained when all other concepts are removed and all that remains is the data about which points lie on which lines. Even with this severe limitation, theorems can be proved and interesting facts emerge concerning this structure. Such fundamental results remain valid when additional concepts are added to form a richer geometry. It sometimes happens that authors blur the distinction between a study and the objects of that study, so it is not surprising to find that some authors refer to incidence structures as incidence geometries.
Tarski's axioms are an axiom system for Euclidean geometry, specifically for that portion of Euclidean geometry that is formulable in first-order logic with identity. As such, it does not require an underlying set theory. The only primitive objects of the system are "points" and the only primitive predicates are "betweenness" and "congruence". The system contains infinitely many axioms.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".
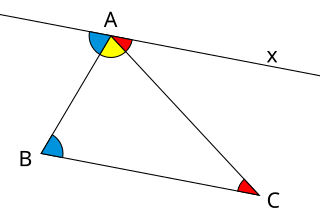
In a Euclidean space, the sum of angles of a triangle equals a straight angle. A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.
In geometry, Pasch's axiom is a statement in plane geometry, used implicitly by Euclid, which cannot be derived from the postulates as Euclid gave them. Its essential role was discovered by Moritz Pasch in 1882.
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.
In geometry, the point–line–plane postulate is a collection of assumptions (axioms) that can be used in a set of postulates for Euclidean geometry in two, three or more dimensions.

Aristotle's axiom is an axiom in the foundations of geometry, proposed by Aristotle in On the Heavens that states:
References
- 1 2 3 Coxeter, H.S.M. (1969). Introduction to Geometry (2nd ed.). John Wiley and Sons. ISBN 0-471-18283-4. Zbl 0181.48101.
- ↑ Heath, Thomas (1956) [1925]. The Thirteen Books of Euclid's Elements (Vol 1) . New York: Dover Publications. pp. 165. ISBN 0-486-60088-2.
- ↑ Pambuccian, Victor (2011). "The axiomatics of ordered geometry: I. Ordered incidence spaces". Expositiones Mathematicae. 29: 24–66. doi:10.1016/j.exmath.2010.09.004.
- ↑ Pambuccian, Victor (2009). "A Reverse Analysis of the Sylvester–Gallai Theorem". Notre Dame Journal of Formal Logic. 50 (3): 245–260. doi: 10.1215/00294527-2009-010 . Zbl 1202.03023.
- ↑ Busemann, Herbert (1955). Geometry of Geodesics. Pure and Applied Mathematics. Vol. 6. New York: Academic Press. p. 139. ISBN 0-12-148350-9. Zbl 0112.37002.