Overspill

Last updated

In non-standard analysis, a branch of mathematics, overspill (referred to as overflow by Goldblatt (1998, p. 129)) is a widely used proof technique. It is based on the fact that the set of standard natural numbers N is not an internal subset of the internal set *N of hypernatural numbers.

Non-standard analysis calculus using a logically rigorous notion of infinitesimal numbers

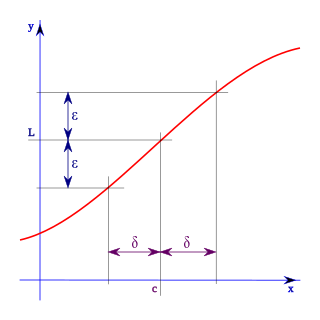
The history of calculus is fraught with philosophical debates about the meaning and logical validity of fluxions or infinitesimal numbers. The standard way to resolve these debates is to define the operations of calculus using epsilon–delta procedures rather than infinitesimals. Non-standard analysis instead reformulates the calculus using a logically rigorous notion of infinitesimal numbers.

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure, space, and change.

Natural number A kind of number, used for counting

In mathematics, the natural numbers are those used for counting and ordering. In common mathematical terminology, words colloquially used for counting are "cardinal numbers" and words connected to ordering represent "ordinal numbers". The natural numbers can, at times, appear as a convenient set of codes ; that is, as what linguists call nominal numbers, foregoing many or all of the properties of being a number in a mathematical sense.

By applying the induction principle for the standard integers N and the transfer principle we get the principle of internal induction:

Mathematical induction form of mathematical proof

Mathematical induction is a mathematical proof technique. It is essentially used to prove that a property P(n) holds for every natural number n, i.e. for n = 0, 1, 2, 3, and so on. Metaphors can be informally used to understand the concept of mathematical induction, such as the metaphor of falling dominoes or climbing a ladder:

Mathematical induction proves that we can climb as high as we like on a ladder, by proving that we can climb onto the bottom rung and that from each rung we can climb up to the next one.

In model theory, a transfer principle states that all statements of some language that are true for some structure are true for another structure. One of the first examples was the Lefschetz principle, which states that any sentence in the first-order language of fields that is true for the complex numbers is also true for any algebraically closed field of characteristic 0.

For any internal subset A of *N, if

  1. 1 is an element of A, and
  2. for every element n of A, n + 1 also belongs to A,

then

A = *N

If N were an internal set, then instantiating the internal induction principle with N, it would follow N = *N which is known not to be the case.

The overspill principle has a number of useful consequences:

Infinitesimal extremely small quantity in calculus; thing so small that there is no way to measure them

In mathematics, infinitesimals are things so small that there is no way to measure them. The insight with exploiting infinitesimals was that entities could still retain certain specific properties, such as angle or slope, even though these entities were quantitatively small. The word infinitesimal comes from a 17th-century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a sequence. Infinitesimals are a basic ingredient in the procedures of infinitesimal calculus as developed by Leibniz, including the law of continuity and the transcendental law of homogeneity. In common speech, an infinitesimal object is an object that is smaller than any feasible measurement, but not zero in size—or, so small that it cannot be distinguished from zero by any available means. Hence, when used as an adjective, "infinitesimal" means "extremely small". To give it a meaning, it usually must be compared to another infinitesimal object in the same context. Infinitely many infinitesimals are summed to produce an integral.

In particular:

Example

These facts can be used to prove the equivalence of the following two conditions for an internal hyperreal-valued function ƒ defined on *R.

and

The proof that the second fact implies the first uses overspill, since given a non-infinitesimal positive ε,

Applying overspill, we obtain a positive appreciable δ with the requisite properties.

These equivalent conditions express the property known in non-standard analysis as S-continuity (or microcontinuity) of ƒ at x. S-continuity is referred to as an external property. The first definition is external because it involves quantification over standard values only. The second definition is external because it involves the external relation of being infinitesimal.

In non-standard analysis, a discipline within classical mathematics, microcontinuity of an internal function f at a point a is defined as follows:

Related Research Articles

In mathematics, a continuous function is a function for which sufficiently small changes in the input result in arbitrarily small changes in the output. Otherwise, a function is said to be a discontinuous function. A continuous function with a continuous inverse function is called a homeomorphism.

In the field of numerical analysis, the condition number of a function with respect to an argument measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input. Very frequently, one is solving the inverse problem – given one is solving for x, and thus the condition number of the (local) inverse must be used. In linear regression the condition number of the moment matrix can be used as a diagnostic for multicollinearity.

Uniform continuity Function limiting the "growth" of distances of outputs uniformly across its domain

In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f(x) and f(y) be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between f(x) and f(y) cannot depend on x and y themselves. For instance, any isometry between metric spaces is uniformly continuous.

Dirac delta function pseudo-function δ such that an integral of δ(x-c)f(x) always takes the value of f(c)

In mathematics, the Dirac delta function is a generalized function or distribution introduced by the physicist Paul Dirac. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by the theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.

Hyperreal number

The system of hyperreal numbers is a way of treating infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form

Squeeze theorem theorem

In calculus, the squeeze theorem, also known as the pinching theorem, the sandwich theorem, the sandwich rule, and sometimes the squeeze lemma, is a theorem regarding the limit of a function.

In mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus. It provides a rigorous justification for some arguments in calculus that were previously considered merely heuristic.

In mathematics, the Heine–Cantor theorem, named after Eduard Heine and Georg Cantor, states that if f : M → N is a continuous function between two metric spaces, and M is compact, then f is uniformly continuous. An important special case is that every continuous function from a bounded closed interval to the real numbers is uniformly continuous.

In numerical analysis, a numerical method is a mathematical tool designed to solve numerical problems. The implementation of a numerical method with an appropriate convergence check in a programming language is called a numerical algorithm.

Elastic energy is the potential mechanical energy stored in the configuration of a material or physical system as work is performed to distort its volume or shape. Elastic energy occurs when objects are compressed and stretched, or generally deformed in any manner. Elasticity theory primarily develops formalisms for the mechanics of solid bodies and materials. The elastic potential energy equation is used in calculations of positions of mechanical equilibrium. The energy is potential as it will be converted into the second form of energy, such as kinetic.

In mathematics, Fermat's theorem is a method to find local maxima and minima of differentiable functions on open sets by showing that every local extremum of the function is a stationary point. Fermat's theorem is a theorem in real analysis, named after Pierre de Fermat.

In mathematics, uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales. The definition used in measure theory is closely related to, but not identical to, the definition typically used in probability.

In non-standard analysis, a field of mathematics, the increment theorem states the following: Suppose a function y = f(x) is differentiable at x and that Δx is infinitesimal. Then

In non-standard analysis, the standard part function is a function from the limited (finite) hyperreal numbers to the real numbers. Briefly, the standard part function "rounds off" a finite hyperreal to the nearest real. It associates to every such hyperreal , the unique real infinitely close to it, i.e. is infinitesimal. As such, it is a mathematical implementation of the historical concept of adequality introduced by Pierre de Fermat, as well as Leibniz's Transcendental law of homogeneity.

(ε, δ)-definition of limit formalization of the notion of limit

In calculus, the (ε, δ)-definition of limit is a formalization of the notion of limit. The concept is due to Augustin-Louis Cauchy, who never gave an definition of limit in his Cours d'Analyse, but occasionally used arguments in proofs. It was first given as a formal definition by Bernard Bolzano in 1817, and the definitive modern statement was ultimately provided by Karl Weierstrass. It makes rigorous the following informal notion: the dependent expression f(x) approaches the value L as the variable x approaches the value c if f(x) can be made as close as desired to L by taking x sufficiently close to c.

In mathematics, the Levi-Civita field, named after Tullio Levi-Civita, is a non-Archimedean ordered field; i.e., a system of numbers containing infinite and infinitesimal quantities. Each member can be constructed as a formal series of the form

The order in probability notation is used in probability theory and statistical theory in direct parallel to the big-O notation that is standard in mathematics. Where the big-O notation deals with the convergence of sequences or sets of ordinary numbers, the order in probability notation deals with convergence of sets of random variables, where convergence is in the sense of convergence in probability.

References

Robert Ian Goldblatt is a mathematical logician who is Emeritus Professor in the School of Mathematics and Statistics at Victoria University, Wellington, New Zealand. His most popular books are Logics of Time and Computation and Topoi: the Categorial Analysis of Logic. He has also written a graduate level textbook on hyperreal numbers which is an introduction to nonstandard analysis.


This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.