

Parastichy, in phyllotaxy, is the spiral pattern of particular plant organs on some plants, such as areoles on cacti stems, florets in sunflower heads and scales in pine cones. [1] These spirals involve the insertion of a single primordium. [2]


Parastichy, in phyllotaxy, is the spiral pattern of particular plant organs on some plants, such as areoles on cacti stems, florets in sunflower heads and scales in pine cones. [1] These spirals involve the insertion of a single primordium. [2]

The common sunflower is a species of large annual forb of the genus Helianthus. It is commonly grown as a crop for its edible oily seeds. Apart from cooking oil production, it is also used as livestock forage, as bird food, in some industrial applications, and as an ornamental in domestic gardens. Wild H. annuus is a widely branched annual plant with many flower heads. The domestic sunflower, however, often possesses only a single large inflorescence atop an unbranched stem.

A pattern is a regularity in the world, in human-made design, or in abstract ideas. As such, the elements of a pattern repeat in a predictable manner. A geometric pattern is a kind of pattern formed of geometric shapes and typically repeated like a wallpaper design.

A Fermat's spiral or parabolic spiral is a plane curve with the property that the area between any two consecutive full turns around the spiral is invariant. As a result, the distance between turns grows in inverse proportion to their distance from the spiral center, contrasting with the Archimedean spiral and the logarithmic spiral. Fermat spirals are named after Pierre de Fermat.
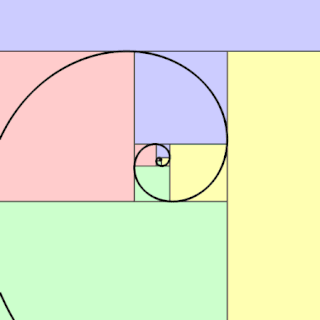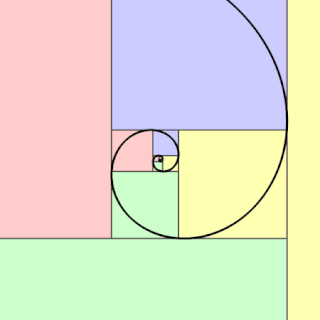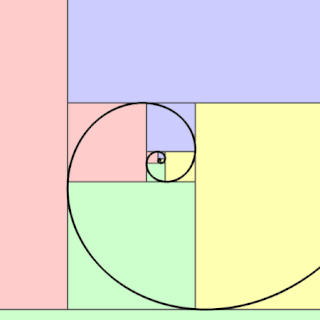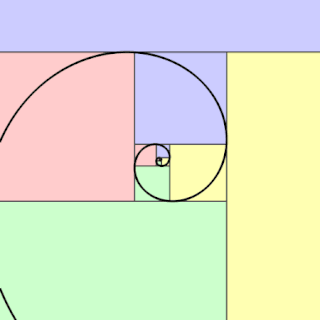
In geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. That is, a golden spiral gets wider by a factor of φ for every quarter turn it makes.

In geometry, the golden angle is the smaller of the two angles created by sectioning the circumference of a circle according to the golden ratio; that is, into two arcs such that the ratio of the length of the smaller arc to the length of the larger arc is the same as the ratio of the length of the larger arc to the full circumference of the circle.

In botany, phyllotaxis or phyllotaxy is the arrangement of leaves on a plant stem. Phyllotactic spirals form a distinctive class of patterns in nature.

Afrocarpus is a genus of conifers of the family Podocarpaceae. Two to six species are recognized. They are evergreen trees native to Africa. Afrocarpus was designated a genus in 1989, when several species formerly classified in Podocarpus and Nageia were reclassified.

On Growth and Form is a book by the Scottish mathematical biologist D'Arcy Wentworth Thompson (1860–1948). The book is long – 793 pages in the first edition of 1917, 1116 pages in the second edition of 1942.

Retrophyllum is a genus of conifers in the family Podocarpaceae. It contains five generally recognized extant species with a disjunct distribution in the Southern Hemisphere, found in Papuasia and also in South America. Retrophyllum are evergreen trees typically occurring in tropical rainforests and cloud forests.
As the tip of a plant shoot grows, new leaves are produced at regular time intervals if temperature is held constant. This time interval is termed the plastochron. The plastochrone index and the leaf plastochron index are ways of measuring the age of a plant dependent on morphological traits rather than on chronological age. Use of these indices removes differences caused by germination, developmental differences and exponential growth.

A primordium in embryology, is an organ or tissue in its earliest recognizable stage of development. Cells of the primordium are called primordial cells. A primordium is the simplest set of cells capable of triggering growth of the would-be organ and the initial foundation from which an organ is able to grow. In flowering plants, a floral primordium gives rise to a flower.

Romanesco broccoli is an edible flower bud of the species Brassica oleracea, which also includes regular broccoli and cauliflower. It is chartreuse in color, and has a form naturally approximating a fractal. Romanesco broccoli has a nutty flavor and a firmer texture than regular broccoli when cooked.

Alexander Carl Heinrich Braun was a German botanist from Regensburg, Bavaria. His research centered on the morphology of plants.

In botany, a whorl or verticil is a whorled arrangement of leaves, sepals, petals, stamens, or carpels that radiate from a single point and surround or wrap around the stem or stalk. A leaf whorl consists of at least three elements; a pair of opposite leaves is not called a whorl.

Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.

This page was created from the Dutch Wikipedia with the aid of automatic translation

Astroloba herrei is a small succulent plant of the genus Astroloba, restricted to the area around the Swartberg mountains, South Africa.

Gonialoe is a small genus of three succulent plant species, indigenous to South Africa, Namibia and Angola. They were formerly included within the related genus Aloe. The three species are Gonialoe variegata, Gonialoe sladeniana, Gonialoe dinteri.

Solving the Riddle of Phyllotaxis: Why the Fibonacci Numbers and the Golden Ratio Occur in Plants is a book on the mathematics of plant structure, and in particular on phyllotaxis, the arrangement of leaves on plant stems. It was written by Irving Adler, and published in 2012 by World Scientific. The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries.

In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes.