
Melting, or fusion, is a physical process that results in the phase transition of a substance from a solid to a liquid. This occurs when the internal energy of the solid increases, typically by the application of heat or pressure, which increases the substance's temperature to the melting point. At the melting point, the ordering of ions or molecules in the solid breaks down to a less ordered state, and the solid melts to become a liquid.

In the physical sciences, a phase is a region of material that is chemically uniform, physically distinct, and (often) mechanically separable. In a system consisting of ice and water in a glass jar, the ice cubes are one phase, the water is a second phase, and the humid air is a third phase over the ice and water. The glass of the jar is a different material, in its own separate phase.

In thermodynamics, the enthalpy of vaporization, also known as the (latent) heat of vaporization or heat of evaporation, is the amount of energy (enthalpy) that must be added to a liquid substance to transform a quantity of that substance into a gas. The enthalpy of vaporization is a function of the pressure and temperature at which the transformation takes place.

Josef Stefan was a Carinthian Slovene physicist, mathematician, and poet of the Austrian Empire.
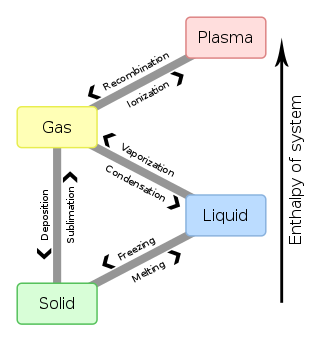
In physics, chemistry, and other related fields like biology, a phase transition is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point.

A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases occur and coexist at equilibrium.

Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects to float on a water surface without becoming even partly submerged.

Benoît Paul Émile Clapeyron was a French engineer and physicist, one of the founders of thermodynamics.

In computational chemistry, molecular physics, and physical chemistry, the Lennard-Jones potential is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is probably the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions. The Lennard-Jones potential is often used as a building block in molecular models for more complex substances. Many studies of the idealized "Lennard-Jones substance" use the potential to understand the physical nature of matter.
In thermodynamics, the phase rule is a general principle governing "pVT" systems, whose thermodynamic states are completely described by the variables pressure, volume and temperature, in thermodynamic equilibrium. If F is the number of degrees of freedom, C is the number of components and P is the number of phases, then
In mathematics and its applications, particularly to phase transitions in matter, a Stefan problem is a particular kind of boundary value problem for a system of partial differential equations (PDE), in which the boundary between the phases can move with time. The classical Stefan problem aims to describe the evolution of the boundary between two phases of a material undergoing a phase change, for example the melting of a solid, such as ice to water. This is accomplished by solving heat equations in both regions, subject to given boundary and initial conditions. At the interface between the phases the temperature is set to the phase change temperature. To close the mathematical system a further equation, the Stefan condition, is required. This is an energy balance which defines the position of the moving interface. Note that this evolving boundary is an unknown (hyper-)surface; hence, Stefan problems are examples of free boundary problems.
Premelting refers to a quasi-liquid film that can occur on the surface of a solid even below melting point. The thickness of the film is temperature dependent. This effect is common for all crystalline materials. Premelting shows its effects in frost heave, and, taking grain boundary interfaces into account, maybe even in the movement of glaciers.
A dispersion is a system in which distributed particles of one material are dispersed in a continuous phase of another material. The two phases may be in the same or different states of matter.
In chemistry, phase-boundary catalysis (PBC) is a type of heterogeneous catalytic system which facilitates the chemical reaction of a particular chemical component in an immiscible phase to react on a catalytic active site located at a phase boundary. The chemical component is soluble in one phase but insoluble in the other. The catalyst for PBC has been designed in which the external part of the zeolite is hydrophobic, internally it is usually hydrophilic, notwithstanding to polar nature of some reactants. In this sense, the medium environment in this system is close to that of an enzyme. The major difference between this system and enzyme is lattice flexibility. The lattice of zeolite is rigid, whereas the enzyme is flexible.
Gunduz Caginalp was a Turkish-born American mathematician whose research has also contributed over 100 papers to physics, materials science and economics/finance journals, including two with Michael Fisher and nine with Nobel Laureate Vernon Smith. He began his studies at Cornell University in 1970 and received an AB in 1973 "Cum Laude with Honors in All Subjects" and Phi Beta Kappa. In 1976 he received a master's degree, and in 1978 a PhD, both also at Cornell. He held positions at The Rockefeller University, Carnegie-Mellon University and the University of Pittsburgh, where he was a professor of Mathematics until his death on December 7, 2021. He was born in Turkey, and spent his first seven years and ages 13–16 there, and the middle years in New York City.

Miscibility or Solubility is the property of two substances to mix in all proportions, forming a homogeneous mixture. Such substances are said to be miscible. The term is most often applied to liquids but also applies to solids and gases. An example in liquids is the miscibility of water and ethanol as they mix in all proportions.
A phase-field model is a mathematical model for solving interfacial problems. It has mainly been applied to solidification dynamics, but it has also been applied to other situations such as viscous fingering, fracture mechanics, hydrogen embrittlement, and vesicle dynamics.
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.
The Gibbs–Thomson effect, in common physics usage, refers to variations in vapor pressure or chemical potential across a curved surface or interface. The existence of a positive interfacial energy will increase the energy required to form small particles with high curvature, and these particles will exhibit an increased vapor pressure. See Ostwald–Freundlich equation. More specifically, the Gibbs–Thomson effect refers to the observation that small crystals are in equilibrium with their liquid melt at a lower temperature than large crystals. In cases of confined geometry, such as liquids contained within porous media, this leads to a depression in the freezing point / melting point that is inversely proportional to the pore size, as given by the Gibbs–Thomson equation.
In mathematics, a free boundary problem is a partial differential equation to be solved for both an unknown function and an unknown domain . The segment of the boundary of which is not known at the outset of the problem is the free boundary.










