Pole splitting

Pole splitting is a phenomenon exploited in some forms of frequency compensation used in an electronic amplifier. When a capacitor is introduced between the input and output sides of the amplifier with the intention of moving the pole lowest in frequency (usually an input pole) to lower frequencies, pole splitting causes the pole next in frequency (usually an output pole) to move to a higher frequency. This pole movement increases the stability of the amplifier and improves its step response at the cost of decreased speed. ^{[1] [2] [3] [4]}

Example of pole splitting

Figure 1: Operational amplifier with compensation capacitor C_C between input and output; notice the amplifier has both input impedance R_i and output impedance R_o.

Figure 2: Operational amplifier with compensation capacitor transformed using Miller's theorem to replace the compensation capacitor with a Miller capacitor at the input and a frequency-dependent current source at the output.

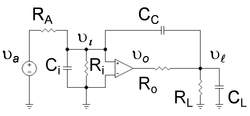
This example shows that introduction of the capacitor referred to as C_C in the amplifier of Figure 1 has two results: first it causes the lowest frequency pole of the amplifier to move still lower in frequency and second, it causes the higher pole to move higher in frequency. ^[5] The amplifier of Figure 1 has a low frequency pole due to the added input resistance R_i and capacitance C_i, with the time constant C_i ( R_A || R_i ). This pole is moved down in frequency by the Miller effect. The amplifier is given a high frequency output pole by addition of the load resistance R_L and capacitance C_L, with the time constant C_L ( R_o || R_L ). The upward movement of the high-frequency pole occurs because the Miller-amplified compensation capacitor C_C alters the frequency dependence of the output voltage divider.

The first objective, to show the lowest pole moves down in frequency, is established using the same approach as the Miller's theorem article. Following the procedure described in the article on Miller's theorem, the circuit of Figure 1 is transformed to that of Figure 2, which is electrically equivalent to Figure 1. Application of Kirchhoff's current law to the input side of Figure 2 determines the input voltage ${\displaystyle \ v_{i}}$ to the ideal op amp as a function of the applied signal voltage ${\displaystyle \ v_{a}}$, namely,

${\displaystyle {\frac {v_{i}}{v_{a}}}={\frac {R_{i}}{R_{i}+R_{A}}}{\frac {1}{1+j\omega (C_{M}+C_{i})(R_{A}\|R_{i})}}\ ,}$

which exhibits a roll-off with frequency beginning at f₁ where

${\displaystyle {\begin{aligned}f_{1}&={\frac {1}{2\pi (C_{M}+C_{i})(R_{A}\|R_{i})}}\\&={\frac {1}{2\pi \tau _{1}}}\ ,\\\end{aligned}}}$

which introduces notation ${\displaystyle \tau _{1}}$ for the time constant of the lowest pole. This frequency is lower than the initial low frequency of the amplifier, which for C_C = 0 F is ${\displaystyle {\frac {1}{2\pi C_{i}(R_{A}\|R_{i})}}}$.

Turning to the second objective, showing the higher pole moves still higher in frequency, it is necessary to look at the output side of the circuit, which contributes a second factor to the overall gain, and additional frequency dependence. The voltage ${\displaystyle \ v_{o}}$ is determined by the gain of the ideal op amp inside the amplifier as

${\displaystyle \ v_{o}=A_{v}v_{i}\ .}$

Using this relation and applying Kirchhoff's current law to the output side of the circuit determines the load voltage ${\displaystyle v_{\ell }}$ as a function of the voltage ${\displaystyle \ v_{i}}$ at the input to the ideal op amp as:

${\displaystyle {\frac {v_{\ell }}{v_{i}}}=A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}\,\!}$${\displaystyle \cdot {\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\ .}$

This expression is combined with the gain factor found earlier for the input side of the circuit to obtain the overall gain as

${\displaystyle {\frac {v_{\ell }}{v_{a}}}={\frac {v_{\ell }}{v_{i}}}{\frac {v_{i}}{v_{a}}}}$

${\displaystyle =A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\,\!}$${\displaystyle \cdot {\frac {1}{1+j\omega (C_{M}+C_{i})(R_{A}\|R_{i})}}\,\!}$${\displaystyle \cdot {\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\ .}$

This gain formula appears to show a simple two-pole response with two time constants. (It also exhibits a zero in the numerator but, assuming the amplifier gain A_v is large, this zero is important only at frequencies too high to matter in this discussion, so the numerator can be approximated as unity.) However, although the amplifier does have a two-pole behavior, the two time-constants are more complicated than the above expression suggests because the Miller capacitance contains a buried frequency dependence that has no importance at low frequencies, but has considerable effect at high frequencies. That is, assuming the output R-C product, C_L ( R_o || R_L ), corresponds to a frequency well above the low frequency pole, the accurate form of the Miller capacitance must be used, rather than the Miller approximation. According to the article on Miller effect, the Miller capacitance is given by

${\displaystyle {\begin{aligned}C_{M}&=C_{C}\left(1-{\frac {v_{\ell }}{v_{i}}}\right)\\&=C_{C}\left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}{\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\right)\ .\\\end{aligned}}}$

(For a positive Miller capacitance, A_v is negative.) Upon substitution of this result into the gain expression and collecting terms, the gain is rewritten as:

${\displaystyle {\frac {v_{\ell }}{v_{a}}}=A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}{\frac {R_{L}}{R_{L}+R_{o}}}{\frac {1+j\omega C_{C}R_{o}/A_{v}}{D_{\omega }}}\ ,}$

with D_ω given by a quadratic in ω, namely:

${\displaystyle D_{\omega }\,\!}$${\displaystyle =[1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})]\,\!}$${\displaystyle \cdot \ [1+j\omega C_{i}(R_{A}\|R_{i})]\,\!}$${\displaystyle \ +j\omega C_{C}(R_{A}\|R_{i})\,\!}$${\displaystyle \cdot \left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{O}}}\right)\,\!}$${\displaystyle \ +(j\omega )^{2}C_{C}C_{L}(R_{A}\|R_{i})(R_{O}\|R_{L})\ .}$

Every quadratic has two factors, and this expression looks simpler if it is rewritten as

${\displaystyle \ D_{\omega }=(1+j\omega {\tau }_{1})(1+j\omega {\tau }_{2})}$

${\displaystyle =1+j\omega ({\tau }_{1}+{\tau }_{2}))+(j\omega )^{2}\tau _{1}\tau _{2}\ ,\ }$

where ${\displaystyle \tau _{1}}$ and ${\displaystyle \tau _{2}}$ are combinations of the capacitances and resistances in the formula for D_ω. ^[6] They correspond to the time constants of the two poles of the amplifier. One or the other time constant is the longest; suppose ${\displaystyle \tau _{1}}$ is the longest time constant, corresponding to the lowest pole, and suppose ${\displaystyle \tau _{1}}$ >> ${\displaystyle \tau _{2}}$. (Good step response requires ${\displaystyle \tau _{1}}$ >> ${\displaystyle \tau _{2}}$. See Selection of C_C below.)

At low frequencies near the lowest pole of this amplifier, ordinarily the linear term in ω is more important than the quadratic term, so the low frequency behavior of D_ω is:

${\displaystyle {\begin{aligned}\ D_{\omega }&=1+j\omega [(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})]\\&=1+j\omega (\tau _{1}+\tau _{2})\approx 1+j\omega \tau _{1}\ ,\ \\\end{aligned}}}$

where now C_M is redefined using the Miller approximation as

${\displaystyle C_{M}=C_{C}\left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}\right)\ ,}$

which is simply the previous Miller capacitance evaluated at low frequencies. On this basis ${\displaystyle \tau _{1}}$ is determined, provided ${\displaystyle \tau _{1}}$ >> ${\displaystyle \tau _{2}}$. Because C_M is large, the time constant ${\displaystyle {\tau }_{1}}$ is much larger than its original value of C_i ( R_A || R_i ). ^[7]

At high frequencies the quadratic term becomes important. Assuming the above result for ${\displaystyle \tau _{1}}$ is valid, the second time constant, the position of the high frequency pole, is found from the quadratic term in D_ω as

${\displaystyle \tau _{2}={\frac {\tau _{1}\tau _{2}}{\tau _{1}}}\approx {\frac {\tau _{1}\tau _{2}}{\tau _{1}+\tau _{2}}}\ .}$

Substituting in this expression the quadratic coefficient corresponding to the product ${\displaystyle \tau _{1}\tau _{2}}$ along with the estimate for ${\displaystyle \tau _{1}}$, an estimate for the position of the second pole is found:

${\displaystyle {\begin{aligned}\tau _{2}&={\frac {(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})(R_{A}\|R_{i})(R_{O}\|R_{L})}{(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})}}\\&\approx {\frac {C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C}}{C_{M}}}(R_{O}\|R_{L})\ ,\\\end{aligned}}}$

and because C_M is large, it seems ${\displaystyle \tau _{2}}$ is reduced in size from its original value C_L ( R_o || R_L ); that is, the higher pole has moved still higher in frequency because of C_C. ^[8]

In short, introduction of capacitor C_C moved the low pole lower and the high pole higher, so the term pole splitting seems a good description.

Selection of C_C

Figure 3: Idealized Bode plot for a two pole amplifier design. Gain drops from first pole at f₁ at 20 dB / decade down to second pole at f₂ where the slope increases to 40 dB / decade.

What value is a good choice for C_C? For general purpose use, traditional design (often called dominant-pole or single-pole compensation) requires the amplifier gain to drop at 20 dB/decade from the corner frequency down to 0 dB gain, or even lower. ^{[9] [10]} With this design the amplifier is stable and has near-optimal step response even as a unity gain voltage buffer. A more aggressive technique is two-pole compensation. ^{[11] [12]}

The way to position f₂ to obtain the design is shown in Figure 3. At the lowest pole f₁, the Bode gain plot breaks slope to fall at 20 dB/decade. The aim is to maintain the 20 dB/decade slope all the way down to zero dB, and taking the ratio of the desired drop in gain (in dB) of 20 log₁₀A_v to the required change in frequency (on a log frequency scale ^[13] ) of ( log₁₀f₂ − log₁₀f₁ ) = log₁₀ ( f₂ / f₁ ) the slope of the segment between f₁ and f₂ is:

Slope per decade of frequency ${\displaystyle =20{\frac {\mathrm {log_{10}} (A_{v})}{\mathrm {log_{10}} (f_{2}/f_{1})}}\ ,}$

which is 20 dB/decade provided f₂ = A_v f₁ . If f₂ is not this large, the second break in the Bode plot that occurs at the second pole interrupts the plot before the gain drops to 0 dB with consequent lower stability and degraded step response.

Figure 3 shows that to obtain the correct gain dependence on frequency, the second pole is at least a factor A_v higher in frequency than the first pole. The gain is reduced a bit by the voltage dividers at the input and output of the amplifier, so with corrections to A_v for the voltage dividers at input and output the pole-ratio condition for good step response becomes:

${\displaystyle {\frac {\tau _{1}}{\tau _{2}}}\approx A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,}$

Figure 4: Miller capacitance at low frequencies C_M (top) and compensation capacitor C_C (bottom) as a function of gain using Excel. Capacitance units are pF.

Using the approximations for the time constants developed above,

${\displaystyle {\frac {\tau _{1}}{\tau _{2}}}\approx {\frac {(\tau _{1}+\tau _{2})^{2}}{\tau _{1}\tau _{2}}}\approx A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,}$

or

${\displaystyle {\frac {[(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})]^{2}}{(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})(R_{A}\|R_{i})(R_{O}\|R_{L})}}\,\!}$${\displaystyle {\color {White}\cdot }=A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,}$

which provides a quadratic equation to determine an appropriate value for C_C. Figure 4 shows an example using this equation. At low values of gain this example amplifier satisfies the pole-ratio condition without compensation (that is, in Figure 4 the compensation capacitor C_C is small at low gain), but as gain increases, a compensation capacitance rapidly becomes necessary (that is, in Figure 4 the compensation capacitor C_C increases rapidly with gain) because the necessary pole ratio increases with gain. For still larger gain, the necessary C_C drops with increasing gain because the Miller amplification of C_C, which increases with gain (see the Miller equation ), allows a smaller value for C_C.

To provide more safety margin for design uncertainties, often A_v is increased to two or three times A_v on the right side of this equation. ^[14] See Sansen ^[4] or Huijsing ^[10] and article on step response.

Slew rate

The above is a small-signal analysis. However, when large signals are used, the need to charge and discharge the compensation capacitor adversely affects the amplifier slew rate; in particular, the response to an input ramp signal is limited by the need to charge C_C.

See also

• Frequency compensation
• Miller effect
• Common source
• Bode plot
• Step response
• CMOS amplifier

References and notes

1. That is, the rise time is selected to be the fastest possible consistent with low overshoot and ringing.
2. C. Toumazu, Moschytz GS & Gilbert B (Editors) (2007). Trade-offs in analog circuit design: the designer's companion. New York/Berlin/Dordrecht: Springer. pp. 272–275. ISBN   978-1-4020-7037-2.{{cite book}}: |author= has generic name (help)
3. Marc T. Thompson (2006). Intuitive analog circuit design: a problem-solving approach using design case studies. Amsterdam: Elsevier Newnes. p. 200. ISBN   0-7506-7786-4.
4. Willy M. C. Sansen (2006). Analog design essentials. New York; Berlin: Springer. pp. §097, p. 266 et seq. ISBN   0-387-25746-2.
5. Although this example appears very specific, the associated mathematical analysis is very much used in circuit design.
6. The sum of the time constants is the coefficient of the term linear in jω and the product of the time constants is the coefficient of the quadratic term in (jω)².
7. The expression for ${\displaystyle \tau _{1}}$ differs a little from ( C_M+C_i ) ( R_A || R_i ) as found initially for f₁, but the difference is minor assuming the load capacitance is not so large that it controls the low frequency response instead of the Miller capacitance.
8. As an aside, the higher the high-frequency pole is made in frequency, the more likely it becomes for a real amplifier that other poles (not considered in this analysis) play a part.
9. A.S. Sedra and K.C. Smith (2004). Microelectronic circuits (Fifth ed.). New York: Oxford University Press. pp. 849 and Example 8.6, p. 853. ISBN   0-19-514251-9.
10. Huijsing, Johan H. (2001). Operational amplifiers: theory and design. Boston, MA: Kluwer Academic. pp. §6.2, pp.205–206 and Figure 6.2.1. ISBN   0-7923-7284-0.
11. Feucht, Dennis: Two-pole compensation
12. Self, Douglas (2006). Audio power amplifier design handbook. Oxford: Newnes. pp. 191–193. ISBN   0-7506-8072-5.
13. That is, the frequency is plotted in powers of ten, as 1, 10, 10²etc.
14. A factor of two results in the maximally flat or Butterworth design for a two-pole amplifier. However, real amplifiers have more than two poles, and a factor greater than two often is necessary.

External links

• Bode Plots in the Circuit Theory Wikibook
• Bode Plots in the Control Systems Wikibook