
In physics, Kaluza–Klein theory is a classical unified field theory of gravitation and electromagnetism built around the idea of a fifth dimension beyond the common 4D of space and time and considered an important precursor to string theory. In their setup, the vacuum has the usual 3 dimensions of space and one dimension of time but with another microscopic extra spatial dimension in the shape of a tiny circle. Gunnar Nordström had an earlier, similar idea. But in that case, a fifth component was added to the electromagnetic vector potential, representing the Newtonian gravitational potential, and writing the Maxwell equations in five dimensions.

The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. This density and flux of energy and momentum are the sources of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity.

Hysteresis is the dependence of the state of a system on its history. For example, a magnet may have more than one possible magnetic moment in a given magnetic field, depending on how the field changed in the past. Plots of a single component of the moment often form a loop or hysteresis curve, where there are different values of one variable depending on the direction of change of another variable. This history dependence is the basis of memory in a hard disk drive and the remanence that retains a record of the Earth's magnetic field magnitude in the past. Hysteresis occurs in ferromagnetic and ferroelectric materials, as well as in the deformation of rubber bands and shape-memory alloys and many other natural phenomena. In natural systems, it is often associated with irreversible thermodynamic change such as phase transitions and with internal friction; and dissipation is a common side effect.

In probability theory and statistics, the Gumbel distribution is used to model the distribution of the maximum of a number of samples of various distributions.
In physics, Ginzburg–Landau theory, often called Landau–Ginzburg theory, named after Vitaly Ginzburg and Lev Landau, is a mathematical physical theory used to describe superconductivity. In its initial form, it was postulated as a phenomenological model which could describe type-I superconductors without examining their microscopic properties. One GL-type superconductor is the famous YBCO, and generally all cuprates.

An electromagnetic four-potential is a relativistic vector function from which the electromagnetic field can be derived. It combines both an electric scalar potential and a magnetic vector potential into a single four-vector.
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.
Scalar–tensor–vector gravity (STVG) is a modified theory of gravity developed by John Moffat, a researcher at the Perimeter Institute for Theoretical Physics in Waterloo, Ontario. The theory is also often referred to by the acronym MOG.
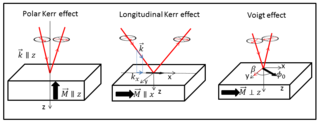
The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. The effect is named after the German scientist Woldemar Voigt who discovered it in vapors. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are also other denominations for this effect, used interchangeably in the modern scientific literature: the Cotton–Mouton effect and magnetic-linear birefringence, with the latter reflecting the physical meaning of the effect.
The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members often asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
A number of different Markov models of DNA sequence evolution have been proposed. These substitution models differ in terms of the parameters used to describe the rates at which one nucleotide replaces another during evolution. These models are frequently used in molecular phylogenetic analyses. In particular, they are used during the calculation of likelihood of a tree and they are used to estimate the evolutionary distance between sequences from the observed differences between the sequences.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.

In probability and statistics, the truncated normal distribution is the probability distribution derived from that of a normally distributed random variable by bounding the random variable from either below or above. The truncated normal distribution has wide applications in statistics and econometrics.
In condensed matter physics, magnetic anisotropy describes how an object's magnetic properties can be different depending on direction. In the simplest case, there is no preferential direction for an object's magnetic moment. It will respond to an applied magnetic field in the same way, regardless of which direction the field is applied. This is known as magnetic isotropy. In contrast, magnetically anisotropic materials will be easier or harder to magnetize depending on which way the object is rotated.
The generalized normal distribution or generalized Gaussian distribution (GGD) is either of two families of parametric continuous probability distributions on the real line. Both families add a shape parameter to the normal distribution. To distinguish the two families, they are referred to below as "symmetric" and "asymmetric"; however, this is not a standard nomenclature.
In probability and statistics, the generalized K-distribution is a three-parameter family of continuous probability distributions. The distribution arises by compounding two gamma distributions. In each case, a re-parametrization of the usual form of the family of gamma distributions is used, such that the parameters are:
In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.

In theoretical physics, Lovelock's theory of gravity (often referred to as Lovelock gravity) is a generalization of Einstein's theory of general relativity introduced by David Lovelock in 1971. It is the most general metric theory of gravity yielding conserved second order equations of motion in an arbitrary number of spacetime dimensions D. In this sense, Lovelock's theory is the natural generalization of Einstein's general relativity to higher dimensions. In three and four dimensions (D = 3, 4), Lovelock's theory coincides with Einstein's theory, but in higher dimensions the theories are different. In fact, for D > 4 Einstein gravity can be thought of as a particular case of Lovelock gravity since the Einstein–Hilbert action is one of several terms that constitute the Lovelock action.
In probability theory and statistics, the noncentral beta distribution is a continuous probability distribution that is a noncentral generalization of the (central) beta distribution.

In theoretical physics, the dual photon is a hypothetical elementary particle that is a dual of the photon under electric–magnetic duality which is predicted by some theoretical models, including M-theory.































