Primitive cell

Last updated April 19, 2021

In geometry, biology, mineralogy, and solid state physics, a primitive cell is a unit cell corresponding to a single lattice point of a structure with discrete translational symmetry. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its primitive cell.

In some cases, the full symmetry of a crystal structure is not obvious from the primitive unit cell, in which cases a conventional cell may be used. A conventional cell (which may or may not be primitive) is the smallest unit cell whose axes follow the symmetry axes of the crystal structure. The volume of the conventional cell is always an integer multiple (typically 1, 2, 3, or 4) of the primitive cell volume. ^[1]

The primitive cell is a primitive place. A primitive unit is a section of the tiling (usually a parallelogram or a set of neighboring tiles) that generates the whole tiling using only translations, and is as small as possible.

The primitive cell is a fundamental domain with respect to translational symmetry only. In the case of additional symmetries a fundamental domain is smaller.

Overview

A crystal can be categorized by its lattice and the atoms that lie in a primitive cell (the basis). A cell will fill all the lattice space without leaving gaps by repetition of crystal translation operations.

By definition, a primitive cell must contain exactly one and only one lattice point. For unit cells generally, lattice points that are shared by $n$ cells are counted as 1/ $n$ of the lattice points contained in each of those cells; so for example a primitive unit cell in three dimensions which has lattice points only at its eight vertices is considered to contain 1/8 of each of them.^[2] An alternative conceptualization is to consistently pick only one of the $n$ lattice points to belong to the given unit cell (so the other $1-n$ lattice points belong to adjacent unit cells).

Two dimensions

A 2-dimensional primitive cell is a parallelogram, which in special cases may have orthogonal angles, or equal lengths, or both.

Conventional primitive cell
Shape name	Parallelogram	Rectangle	Square
Bravais lattice	Primitive Oblique	Primitive Rectangular	Primitive Square

The centered rectangular lattice also has a primitive cell in the shape of a rhombus, but in order to allow easy discrimination on the basis of symmetry, it is represented by a conventional cell which contains two lattice points.

Primitive cell
Shape name	Rhombus
Conventional cell
Bravais lattice	Centered Rectangular

Three dimensions

The primitive translation vectors $a \to 1$ , $a \to 2$ , $a \to 3$ span a lattice cell of smallest volume for a particular three-dimensional lattice, and are used to define a crystal translation vector

{\vec {T}}=u_{1}{\vec {a}}_{1}+u_{2}{\vec {a}}_{2}+u_{3}{\vec {a}}_{3},

where $u 1$ , $u 2$ , $u 3$ are integers, translation by which leaves the lattice invariant.^{[note 1]} That is, for a point in the lattice $r$ , the arrangement of points appears the same from $r' = r + T \to$ as from $r$ .^[3]

Since the primitive cell is defined by the primitive axes (vectors) $a \to 1$ , $a \to 2$ , $a \to 3$ , the volume $V p$ of the primitive cell is given by the parallelepiped from the above axes as

V_{\mathrm {p} }=\left|{\vec {a}}_{1}\cdot ({\vec {a}}_{2}\times {\vec {a}}_{3})\right|.

For any 3-dimensional lattice, you can find primitive cells which are parallelepipeds, which in special cases may have orthogonal angles, or equal lengths, or both. While not mathematically required, by convention, one usually defines the parallelepiped primitive cell so that there is a lattice point on each corner. When the lattice points are on the corner, each lattice point is shared by eight different primitive cells, so each lattice point will contribute only 1/8 of a lattice point to each of those cells. However, there are eight corners, so there is still a total of one lattice point per cell, as required by definition. Some of the fourteen three-dimensional Bravais lattices are represented using such parallelepiped primitive cells, as shown below.

Conventional primitive cell
Shape name	Parallelepiped	Oblique rectangular prism	Rectangular cuboid	Square cuboid	Trigonal trapezohedron	Cube
Bravais lattice	Primitive Triclinic	Primitive Monoclinic	Primitive Orthorhombic	Primitive Tetragonal	Primitive Rhombohedral	Primitive Cubic

The other Bravais lattices also have primitive cells in the shape of a parallelepiped, but in order to allow easy discrimination on the basis of symmetry, they are represented by conventional cells which contain more than one lattice point.

Primitive cell
Shape name	Oblique rhombic prism	Right rhombic prism
Conventional cell
Bravais lattice	Base-centered Monoclinic	Base-centered Orthorhombic

Wigner–Seitz cell

An alternative to the unit cell, for every Bravais lattice there is another kind of primitive cell called the Wigner–Seitz cell. In the Wigner–Seitz cell, the lattice point is at the center of the cell, and for most Bravais lattices, the shape is not a parallelogram or parallelepiped. This is a type of Voronoi cell. The Wigner–Seitz cell of the reciprocal lattice in momentum space is called the Brillouin zone.

Notes

↑ In $n$ dimensions the crystal translation vector would be
${\vec {T}}=\sum _{i=1}^{n}u_{i}{\vec {a}}_{i},\quad {\mbox{where }}u_{i}\in \mathbb {Z} \quad \forall i.$
That is, for a point in the lattice $r$ , the arrangement of points appears the same from $r' = r + T \to$ as from $r$ .

Related Research Articles

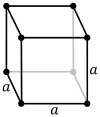
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, the four concepts—parallelepiped and cube in three dimensions, parallelogram and square in two dimensions—are defined, but in the context of a more general affine geometry, in which angles are not differentiated, only parallelograms and parallelepipeds exist. Three equivalent definitions of parallelepiped are

Crystal structure Ordered arrangement of atoms, ions, or molecules in a crystalline material

In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles and tiles as well as wallpaper.

In crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals. Informally, two crystals are in the same crystal system if they have similar symmetries, although there are many exceptions to this.

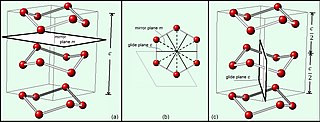
In mathematics, physics and chemistry, a space group is the symmetry group of a configuration in space, usually in three dimensions. In three dimensions, there are 219 distinct types, or 230 if chiral copies are considered distinct. Space groups are also studied in dimensions other than 3 where they are sometimes called Bieberbach groups, and are discrete cocompact groups of isometries of an oriented Euclidean space.

In geometry and group theory, a lattice in is a subgroup of the additive group $which is isomorphic to the additive group, and which spans the real vector space . In other words, for any basis of, the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice. A lattice may be viewed as a regular tiling of a space by a primitive cell.$

Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits.

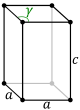
In crystallography, the monoclinic crystal system is one of the seven crystal systems. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a rectangular prism with a parallelogram as its base. Hence two pairs of vectors are perpendicular, while the third pair makes an angle other than 90°.

In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.

In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. In the same way the Bravais lattice is divided up into Wigner–Seitz cells in the real lattice, the reciprocal lattice is broken up into Brillouin zones. The boundaries of this cell are given by planes related to points on the reciprocal lattice. The importance of the Brillouin zone stems from the description of waves in a periodic medium given by Bloch's theorem, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone.

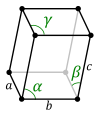
In geometry and crystallography, a Bravais lattice, named after Auguste Bravais (1850), is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by:

In physics, the reciprocal lattice represents the Fourier transform of another lattice. In normal usage, the initial lattice is usually a periodic spatial function in real-space and is also known as the direct lattice. While the direct lattice exists in real-space and is what one would commonly understand as a physical lattice, the reciprocal lattice exists in reciprocal space. The reciprocal lattice of a reciprocal lattice is equivalent to the original direct lattice, because the defining equations are symmetrical with respect to the vectors in real and reciprocal space. Mathematically, direct and reciprocal lattice vectors represent covariant and contravariant vectors, respectively.

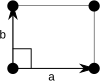
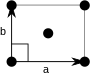
In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by a: T_a(p) = p + a.

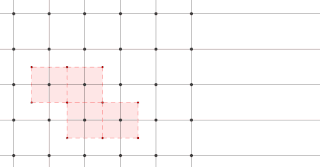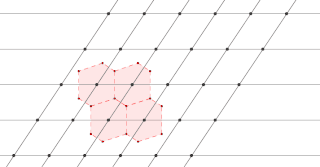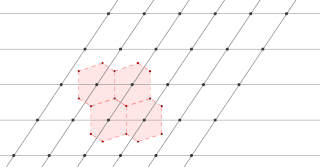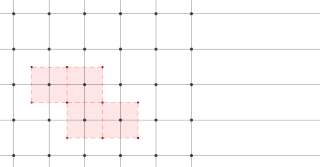
The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in solid-state physics.

In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin. This notation is sometimes called international notation, because it was adopted as standard by the International Tables For Crystallography since their first edition in 1935.

In solid-state physics and crystallography, a crystal structure is described by a unit cell. There are an infinite number of unit cells with different shapes and sizes which can describe the same crystal. Say that a crystal structure is described by a unit cell U. The supercell S of unit cell U is a cell which describes the same crystal, but has larger volume than cell U. Many methods which use a supercell perturbate it somehow to determine properties which cannot be determined by the initial cell. For example, during phonon calculations by the small displacement method, phonon frequencies in crystals are calculated using force values on slightly displaced atoms in the supercell. Another very important example of a supercell is the conventional cell of body-centered (bcc) or face-centered (fcc) cubic crystals.

The Pearson symbol, or Pearson notation, is used in crystallography as a means of describing a crystal structure, and was originated by W.B. Pearson. The symbol is made up of two letters followed by a number. For example:

In crystallography, the hexagonal crystal family is one of the six crystal families, which includes two crystal systems and two lattice systems. While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent. In particular, there are crystals with trigonal symmetry but belong to the hexagonal lattice.

In geometry a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron.

References

↑ Ashcroft, Neil W. (1976). Solid State Physics . W. B. Saunders Company. p. 73. ISBN 0-03-083993-9.
↑ "DoITPoMS – TLP Library Crystallography – Unit Cell". Online Materials Science Learning Resources: DoITPoMS. University of Cambridge. Retrieved 21 February 2015.
↑ Kittel, Charles. Introduction to Solid State Physics (8 ed.). Wiley. p. 4. ISBN 978-0-471-41526-8.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[first-3] In $n$ dimensions the crystal translation vector would be
${\vec {T}}=\sum _{i=1}^{n}u_{i}{\vec {a}}_{i},\quad {\mbox{where }}u_{i}\in \mathbb {Z} \quad \forall i.$
That is, for a point in the lattice $r$ , the arrangement of points appears the same from $r' = r + T \to$ as from $r$ .

[1] Ashcroft, Neil W. (1976). Solid State Physics . W. B. Saunders Company. p. 73. ISBN 0-03-083993-9.

[doitpoms-2] "DoITPoMS – TLP Library Crystallography – Unit Cell". Online Materials Science Learning Resources: DoITPoMS. University of Cambridge. Retrieved 21 February 2015.

[4] Kittel, Charles. Introduction to Solid State Physics (8 ed.). Wiley. p. 4. ISBN 978-0-471-41526-8.

[1]

[2]

[note 1]

[3]