In crystallography, the monoclinic crystal system is one of the seven crystal systems. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a parallelogram prism. Hence two pairs of vectors are perpendicular (meet at right angles), while the third pair makes an angle other than 90°.
Two monoclinic Bravais lattices exist: the primitive monoclinic and the base-centered monoclinic.
| Bravais lattice | Primitive monoclinic | Base-centered monoclinic |
|---|---|---|
| Pearson symbol | mP | mS |
| Unit cell |  |  |
For the base-centered monoclinic lattice, the primitive cell has the shape of an oblique rhombic prism; [1] it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. The length of the primitive cell below equals of the conventional cell above.
The table below organizes the space groups of the monoclinic crystal system by crystal class. It lists the International Tables for Crystallography space group numbers, [2] followed by the crystal class name, its point group in Schoenflies notation, Hermann–Mauguin (international) notation, orbifold notation, and Coxeter notation, type descriptors, mineral examples, and the notation for the space groups.
| # | Point group | Type | Example | Space groups | |||||
|---|---|---|---|---|---|---|---|---|---|
| Name [3] | Schön. | Intl | Orb. | Cox. | Primitive | Base-centered | |||
| 3–5 | Sphenoidal | C2 | 2 | 22 | [2]+ | enantiomorphic polar | halotrichite | P2, P21 | C2 |
| 6–9 | Domatic | Cs (C1h) | m | *11 | [ ] | polar | hilgardite | Pm, Pc | Cm, Cc |
| 10–12 | Prismatic | C2h | 2/m | 2* | [2,2+] | centrosymmetric | gypsum | P2/m, P21/m | C2/m |
| 13–15 | P2/c, P21/c | C2/c | |||||||
Sphenoidal is also called monoclinic hemimorphic, domatic is also called monoclinic hemihedral, and prismatic is also called monoclinic normal.
The three monoclinic hemimorphic space groups are as follows:
The four monoclinic hemihedral space groups include
The only monoclinic Bravais lattice in two dimensions is the oblique lattice.
| Bravais lattice | Oblique |
|---|---|
| Pearson symbol | mp |
| Unit cell |  |
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.
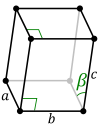
In crystallography, the tetragonal crystal system is one of the 7 crystal systems. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base (a by a) and height (c, which is different from a).
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed.
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tiles, and wallpaper.
In geometry, a glide reflection or transflection is a geometric transformation that consists of a reflection across a hyperplane and a translation ("glide") in a direction parallel to that hyperplane, combined into a single transformation. Because the distances between points are not changed under glide reflection, it is a motion or isometry. When the context is the two-dimensional Euclidean plane, the hyperplane of reflection is a straight line called the glide line or glide axis. When the context is three-dimensional space, the hyperplane of reflection is a plane called the glide plane. The displacement vector of the translation is called the glide vector.
In crystallography, a crystal system is a set of point groups. A lattice system is a set of Bravais lattices. Space groups are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family.
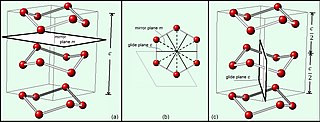
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.
In geometry and crystallography, a Bravais lattice, named after Auguste Bravais, is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
In crystallography, a crystallographic point group is a three dimensional point group whose symmetry operations are compatible with a three dimensional crystallographic lattice. According to the crystallographic restriction it may only contain one-, two-, three-, four- and sixfold rotations or rotoinversions. This reduces the number of crystallographic point groups to 32. These 32 groups are one-and-the-same as the 32 types of morphological (external) crystalline symmetries derived in 1830 by Johann Friedrich Christian Hessel from a consideration of observed crystal forms.
In crystallography, the tricliniccrystal system is one of the seven crystal systems. A crystal system is described by three basis vectors. In the triclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. In addition, the angles between these vectors must all be different and may not include 90°.
In crystallography, the cubiccrystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals.
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices.
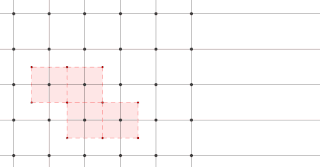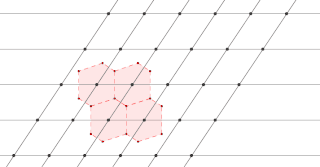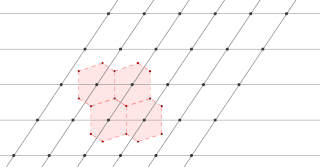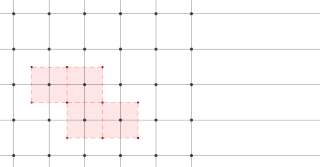
The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in crystallography.
In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin. This notation is sometimes called international notation, because it was adopted as standard by the International Tables For Crystallography since their first edition in 1935.
In crystallography, the hexagonal crystal family is one of the six crystal families, which includes two crystal systems and two lattice systems. While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent. In particular, there are crystals that have trigonal symmetry but belong to the hexagonal lattice.
In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron.
The rectangular lattice and rhombic lattice constitute two of the five two-dimensional Bravais lattice types. The symmetry categories of these lattices are wallpaper groups pmm and cmm respectively. The conventional translation vectors of the rectangular lattices form an angle of 90° and are of unequal lengths.
| Seven 3D systems |
|
|---|---|
| Four 2D systems | |
