 |  |
| Primitive | Centered |
|---|---|
 |  |
| pmm | cmm |
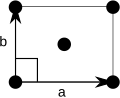
The rectangular lattice and rhombic lattice (or centered rectangular lattice) constitute two of the five two-dimensional Bravais lattice types. [1] The symmetry categories of these lattices are wallpaper groups pmm and cmm respectively. The conventional translation vectors of the rectangular lattices form an angle of 90° and are of unequal lengths.
There are two rectangular Bravais lattices: primitive rectangular and centered rectangular (also rhombic).
| Bravais lattice | Rectangular | Centered rectangular |
|---|---|---|
| Pearson symbol | op | oc |
| Standard unit cell |  |  |
| Rhombic unit cell |  |  |
The primitive rectangular lattice can also be described by a centered rhombic unit cell, while the centered rectangular lattice can also be described by a primitive rhombic unit cell. Note that the length in the lower row is not the same as in the upper row. For the first column above, of the second row equals of the first row, and for the second column it equals .
The rectangular lattice class names, Schönflies notation, Hermann-Mauguin notation, orbifold notation, Coxeter notation, and wallpaper groups are listed in the table below.
| Geometric class, point group | Arithmetic class | Wallpaper groups | ||||
|---|---|---|---|---|---|---|
| Schön. | Intl | Orb. | Cox. | |||
| D1 | m | (*) | [ ] | Along | pm (**) | pg (××) |
| Between | cm (*×) | |||||
| D2 | 2mm | (*22) | [2] | Along | pmm (*2222) | pmg (22*) |
| Between | cmm (2*22) | pgg (22×) | ||||
In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. In Euclid's Elements, definition 22 defines a rhombus as "Of quadrilateral figures, a rhombus that which is equilateral but not right-angled." Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.
In crystallography, the tetragonal crystal system is one of the 7 crystal systems. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base and height.
In geometry, biology, mineralogy, and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed.
A wallpaper is a mathematical object we imagine covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. To a given wallpaper there corresponds a group of such congruent transformations, with function composition as the group operation. Thus, a wallpaper group is in a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations and tiles as well as wallpaper.
In mathematics, physics and chemistry, a space group is the symmetry group of an object in space, usually in three dimensions. The elements of a space group are the rigid transformations of an object that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.
In geometry and group theory, a lattice in the real coordinate space is an infinite set of points in this space with the properties that coordinatewise addition or subtraction of two points in the lattice produces another lattice point, that the lattice points are all separated by some minimum distance, and that every point in the space is within some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the points in the space, and the requirements of minimum and maximum distance can be summarized by saying that a lattice is a Delone set. More abstractly, a lattice can be described as a free abelian group of dimension which spans the vector space . For any basis of , the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice, and every lattice can be formed from a basis in this way. A lattice may be viewed as a regular tiling of a space by a primitive cell.
In crystallography, the monoclinic crystal system is one of the seven crystal systems. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a rectangular prism with a parallelogram as its base. Hence two pairs of vectors are perpendicular, while the third pair makes an angle other than 90°.
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.
In geometry and crystallography, a Bravais lattice, named after Auguste Bravais (1850), is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
In physics, the reciprocal lattice represents the Fourier transform of another lattice. In normal usage, the initial lattice is usually a periodic spatial function in real-space and is also known as the direct lattice. While the direct lattice exists in real-space and is what one would commonly understand as a physical lattice, the reciprocal lattice exists in reciprocal space. The reciprocal lattice of a reciprocal lattice is equivalent to the original direct lattice, because the defining equations are symmetrical with respect to the vectors in real and reciprocal space. Mathematically, direct and reciprocal lattice vectors represent covariant and contravariant vectors, respectively.
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement. Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices.
The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in the crystallography.
In geometry, a rhombic enneacontahedron is a polyhedron composed of 90 rhombic faces; with three, five, or six rhombi meeting at each vertex. It has 60 broad rhombi and 30 slim. The rhombic enneacontahedron is a zonohedron with a superficial resemblance to the rhombic triacontahedron.
The hexagonal lattice or triangular lattice is one of the five two-dimensional Bravais lattice types. The symmetry category of the lattice is wallpaper group p6m. The primitive translation vectors of the hexagonal lattice form an angle of 120° and are of equal lengths,
The Pearson symbol, or Pearson notation, is used in crystallography as a means of describing a crystal structure, and was originated by W. B. Pearson. The symbol is made up of two letters followed by a number. For example:
In crystallography, the hexagonal crystal family is one of the six crystal families, which includes two crystal systems and two lattice systems. While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent. In particular, there are crystals that have trigonal symmetry but belong to the hexagonal lattice.
| Seven 3D systems |
|
|---|---|
| Four 2D systems | |
