
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal transformations. Clifford algebras have important applications in a variety of fields including geometry, theoretical physics and digital image processing. They are named after the English mathematician William Kingdon Clifford.

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.

In mathematics, the orthogonal group in dimension n, denoted O(n), is the group of distance-preserving transformations of a Euclidean space of dimension n that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of n×n orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.

In mathematics, the unitary group of degree n, denoted U(n), is the group of n × n unitary matrices, with the group operation of matrix multiplication. The unitary group is a subgroup of the general linear group GL(n, C). Hyperorthogonal group is an archaic name for the unitary group, especially over finite fields. For the group of unitary matrices with determinant 1, see Special unitary group.

In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz.

In mathematics and theoretical physics, a representation of a Lie group is a linear action of a Lie group on a vector space. Equivalently, a representation is a smooth homomorphism of the group into the group of invertible operators on the vector space. Representations play an important role in the study of continuous symmetry. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie algebras.

In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts transitively. The elements of G are called the symmetries of X. A special case of this is when the group G in question is the automorphism group of the space X – here "automorphism group" can mean isometry group, diffeomorphism group, or homeomorphism group. In this case, X is homogeneous if intuitively X looks locally the same at each point, either in the sense of isometry, diffeomorphism, or homeomorphism (topology). Some authors insist that the action of G be faithful, although the present article does not. Thus there is a group action of G on X which can be thought of as preserving some "geometric structure" on X, and making X into a single G-orbit.

In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P(V). Explicitly, the projective linear group is the quotient group

In mathematics the spin group Spin(n) is the double cover of the special orthogonal group SO(n) = SO(n, R), such that there exists a short exact sequence of Lie groups

In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections, the associated holonomy is a type of monodromy and is an inherently global notion. For curved connections, holonomy has nontrivial local and global features.
In group theory, restriction forms a representation of a subgroup using a known representation of the whole group. Restriction is a fundamental construction in representation theory of groups. Often the restricted representation is simpler to understand. Rules for decomposing the restriction of an irreducible representation into irreducible representations of the subgroup are called branching rules, and have important applications in physics. For example, in case of explicit symmetry breaking, the symmetry group of the problem is reduced from the whole group to one of its subgroups. In quantum mechanics, this reduction in symmetry appears as a splitting of degenerate energy levels into multiplets, as in the Stark or Zeeman effect.
In mathematics, real projective space, or RPn or , is the topological space of lines passing through the origin 0 in Rn+1. It is a compact, smooth manifold of dimension n, and is a special case Gr(1, Rn+1) of a Grassmannian space.
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group.
In differential geometry, a spin structure on an orientable Riemannian manifold (M, g) allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry.
In mathematics, the projective unitary groupPU(n) is the quotient of the unitary group U(n) by the right multiplication of its center, U(1), embedded as scalars. Abstractly, it is the holomorphic isometry group of complex projective space, just as the projective orthogonal group is the isometry group of real projective space.

In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of n-dimensional hyperbolic geometry in which points are represented by points on the forward sheet S+ of a two-sheeted hyperboloid in (n+1)-dimensional Minkowski space or by the displacement vectors from the origin to those points, and m-planes are represented by the intersections of (m+1)-planes passing through the origin in Minkowski space with S+ or by wedge products of m vectors. Hyperbolic space is embedded isometrically in Minkowski space; that is, the hyperbolic distance function is inherited from Minkowski space, analogous to the way spherical distance is inherited from Euclidean distance when the n-sphere is embedded in (n+1)-dimensional Euclidean space.

In geometry, a point reflection is a type of isometry of Euclidean space. An object that is invariant under a point reflection is said to possess point symmetry; if it is invariant under point reflection through its center, it is said to possess central symmetry or to be centrally symmetric.
In geometry, a (globally) projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids.
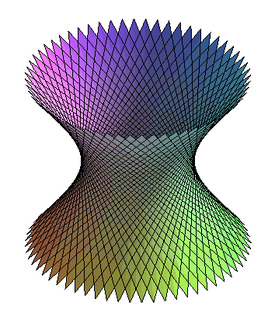
In mathematics, a quadric or quadric hypersurface is the subspace of N-dimensional space defined by a polynomial equation of degree 2 over a field. Quadrics are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space. An example is the quadric surface


























