
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation for an arbitrary complex number , which represents the order of the Bessel function. Although and produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of .
Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral

In mathematics, a trigonometric substitution replaces a trigonometric function for another expression. In calculus, trigonometric substitutions are a technique for evaluating integrals. In this case, an expression involving a radical function is replaced with a trigonometric one. Trigonometric identities may help simplify the answer. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.

In mathematics, the Clausen function, introduced by Thomas Clausen, is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.

In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. Theta functions are parametrized by points in a tube domain inside a complex Lagrangian Grassmannian, namely the Siegel upper half space.
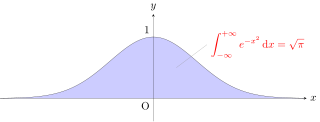
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real number line.

In mathematics, the Z function is a function used for studying the Riemann zeta function along the critical line where the argument is one-half. It is also called the Riemann–Siegel Z function, the Riemann–Siegel zeta function, the Hardy function, the Hardy Z function and the Hardy zeta function. It can be defined in terms of the Riemann–Siegel theta function and the Riemann zeta function by
In geometry, the area enclosed by a circle of radius r is πr2. Here, the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.
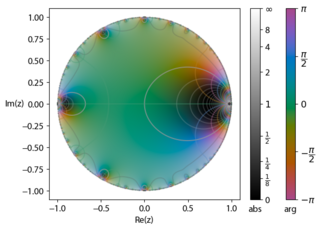
In mathematics, the Euler function is given by
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Wilhelm Leibniz, states that for an integral of the form where and the integrands are functions dependent on the derivative of this integral is expressible as where the partial derivative indicates that inside the integral, only the variation of with is considered in taking the derivative.

The Rogers–Ramanujan continued fraction is a continued fraction discovered by Rogers (1894) and independently by Srinivasa Ramanujan, and closely related to the Rogers–Ramanujan identities. It can be evaluated explicitly for a broad class of values of its argument.

Landen's transformation is a mapping of the parameters of an elliptic integral, useful for the efficient numerical evaluation of elliptic functions. It was originally due to John Landen and independently rediscovered by Carl Friedrich Gauss.
In integral calculus, the tangent half-angle substitution is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of into an ordinary rational function of by setting . This is the one-dimensional stereographic projection of the unit circle parametrized by angle measure onto the real line. The general transformation formula is:

In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities,

In physics, engineering, and applied mathematics, the Bickley–Naylor functions are a sequence of special functions arising in formulas for thermal radiation intensities in hot enclosures. The solutions are often quite complicated unless the problem is essentially one-dimensional. These functions have practical applications in several engineering problems related to transport of thermal or neutron, radiation in systems with special symmetries. W. G. Bickley was a British mathematician born in 1893.























