
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.
In linear algebra, the Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g., Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices, and posthumously published in 1924. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations.
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by .
In mathematics, Thurston's geometrization conjecture states that each of certain three-dimensional topological spaces has a unique geometric structure that can be associated with it. It is an analogue of the uniformization theorem for two-dimensional surfaces, which states that every simply connected Riemann surface can be given one of three geometries . In three dimensions, it is not always possible to assign a single geometry to a whole topological space. Instead, the geometrization conjecture states that every closed 3-manifold can be decomposed in a canonical way into pieces that each have one of eight types of geometric structure. The conjecture was proposed by William Thurston, and implies several other conjectures, such as the Poincaré conjecture and Thurston's elliptization conjecture.

Nonlinear dimensionality reduction, also known as manifold learning, is any of various related techniques that aim to project high-dimensional data onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis.

In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classification of closed surfaces.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
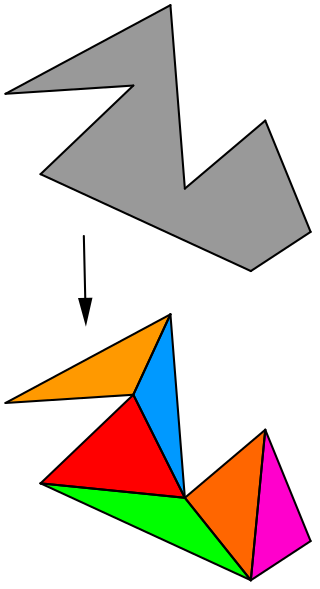
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.

In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds. Handles are used to particularly study 3-manifolds.

In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
Algorithmic topology, or computational topology, is a subfield of topology with an overlap with areas of computer science, in particular, computational geometry and computational complexity theory.

In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.
SnapPea is free software designed to help mathematicians, in particular low-dimensional topologists, study hyperbolic 3-manifolds. The primary developer is Jeffrey Weeks, who created the first version as part of his doctoral thesis, supervised by William Thurston. It is not to be confused with the unrelated android malware with the same name.
In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique finite collection of prime 3-manifolds.

In mathematics, a normal surface is a surface inside a triangulated 3-manifold that intersects each tetrahedron in several components called normal disks. Each normal disk is a triangle which cuts off a vertex of the tetrahedron, or a quad which separates pairs of vertices. Thus, in a given tetrahedron there cannot be two quads separating different pairs of vertices, since such quads would intersect in a line, meaning the surface would be self-intersecting.

Joachim Hyam Rubinstein FAA is an Australian top mathematician specialising in low-dimensional topology; he is currently serving as an honorary professor in the Department of Mathematics and Statistics at the University of Melbourne, having retired in 2019.
In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non boundary-parallel torus in its complement. Every knot is either hyperbolic, a torus, or a satellite knot. The class of satellite knots include composite knots, cable knots, and Whitehead doubles. A satellite link is one that orbits a companion knot K in the sense that it lies inside a regular neighborhood of the companion.
In topology, a branch of mathematics, a prime manifold is an n-manifold that cannot be expressed as a non-trivial connected sum of two n-manifolds. Non-trivial means that neither of the two is an n-sphere. A similar notion is that of an irreduciblen-manifold, which is one in which any embedded (n − 1)-sphere bounds an embedded n-ball. Implicit in this definition is the use of a suitable category, such as the category of differentiable manifolds or the category of piecewise-linear manifolds.











