A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference.
In geometry, an equilateral polygon is a polygon which has all sides of the same length. Except in the triangle case, an equilateral polygon does not need to also be equiangular, but if it does then it is a regular polygon. If the number of sides is at least five, an equilateral polygon does not need to be a convex polygon: it could be concave or even self-intersecting.

In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple or star polygons.

In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

In geometry, a curve of constant width is a simple closed curve in the plane whose width is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve.

A Reuleaux triangle is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

In geometry, Barbier's theorem states that every curve of constant width has perimeter π times its width, regardless of its precise shape. This theorem was first published by Joseph-Émile Barbier in 1860.

In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. It is a circular arc that measures 180°. It has only one line of symmetry.

In geometry, a convex polygon is a polygon that is the boundary of a convex set. This means that the line segment between two points of the polygon is contained in the union of the interior and the boundary of the polygon. In particular, it is a simple polygon. Equivalently, a polygon is convex if every line that does not contain any edge intersects the polygon in at most two points.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.

In geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figure F is inscribed in figure G" means precisely the same thing as "figure G is circumscribed about figure F". A circle or ellipse inscribed in a convex polygon is tangent to every side or face of the outer figure. A polygon inscribed in a circle, ellipse, or polygon has each vertex on the outer figure; if the outer figure is a polygon or polyhedron, there must be a vertex of the inscribed polygon or polyhedron on each side of the outer figure. An inscribed figure is not necessarily unique in orientation; this can easily be seen, for example, when the given outer figure is a circle, in which case a rotation of an inscribed figure gives another inscribed figure that is congruent to the original one.

The four-vertex theorem of geometry states that the curvature along a simple, closed, smooth plane curve has at least four local extrema. The name of the theorem derives from the convention of calling an extreme point of the curvature function a vertex. This theorem has many generalizations, including a version for space curves where a vertex is defined as a point of vanishing torsion.

The Reuleaux tetrahedron is the intersection of four balls of radius s centered at the vertices of a regular tetrahedron with side length s. The spherical surface of the ball centered on each vertex passes through the other three vertices, which also form vertices of the Reuleaux tetrahedron. Thus the center of each ball is on the surfaces of the other three balls. The Reuleaux tetrahedron has the same face structure as a regular tetrahedron, but with curved faces: four vertices, and four curved faces, connected by six circular-arc edges.

In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. It is a special case of an arc, with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum) above the symbols for the two endpoints, such as in AB.

In plane geometry the Blaschke–Lebesgue theorem states that the Reuleaux triangle has the least area of all curves of given constant width. In the form that every curve of a given width has area at least as large as the Reuleaux triangle, it is also known as the Blaschke–Lebesgue inequality. It is named after Wilhelm Blaschke and Henri Lebesgue, who published it separately in the early 20th century.
In geometry, a circular triangle is a triangle with circular arc edges.
In geometry, a polycon is a kind of a developable roller. It is made of identical pieces of a cone whose apex angle equals the angle of an even sided regular polygon. In principle, there are infinitely many polycons, as many as there are even sided regular polygons. Most members of the family have elongated spindle like shapes. The polycon family generalizes the sphericon. It was discovered by the Israeli inventor David Hirsch in 2017
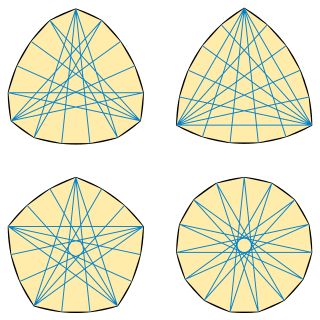
In geometry, a Reinhardt polygon is an equilateral polygon inscribed in a Reuleaux polygon. As in the regular polygons, each vertex of a Reinhardt polygon participates in at least one defining pair of the diameter of the polygon. Reinhardt polygons with sides exist, often with multiple forms, whenever is not a power of two. Among all polygons with sides, the Reinhardt polygons have the largest possible perimeter for their diameter, the largest possible width for their diameter, and the largest possible width for their perimeter. They are named after Karl Reinhardt, who studied them in 1922.



















