
In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by at most one path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees.

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at least one edge out of every cycle in the graph. Removing these edges from the graph breaks all of the cycles, producing an acyclic subgraph of the given graph, often called a directed acyclic graph. A feedback arc set with the fewest possible edges is a minimum feedback arc set and its removal leaves a maximum acyclic subgraph; weighted versions of these optimization problems are also used. If a feedback arc set is minimal, meaning that removing any edge from it produces a subset that is not a feedback arc set, then it has an additional property: reversing all of its edges, rather than removing them, produces a directed acyclic graph.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

David Michael Avis is a Canadian and British computer scientist known for his contributions to geometric computations. Avis is a professor in computational geometry and applied mathematics in the School of Computer Science, McGill University, in Montreal. Since 2010, he belongs to Department of Communications and Computer Engineering, School of Informatics, Kyoto University.
In mathematics, the vertex enumeration problem for a polytope, a polyhedral cell complex, a hyperplane arrangement, or some other object of discrete geometry, is the problem of determination of the object's vertices given some formal representation of the object. A classical example is the problem of enumeration of the vertices of a convex polytope specified by a set of linear inequalities:
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

polymake is software for the algorithmic treatment of convex polyhedra.
In graph theory, a Trémaux tree of an undirected graph is a type of spanning tree, generalizing depth-first search trees. They are defined by the property that every edge of connects an ancestor–descendant pair in the tree. Trémaux trees are named after Charles Pierre Trémaux, a 19th-century French author who used a form of depth-first search as a strategy for solving mazes. They have also been called normal spanning trees, especially in the context of infinite graphs.
In graph theory, a partial cube is a graph that is isometric to a subgraph of a hypercube. In other words, a partial cube can be identified with a subgraph of a hypercube in such a way that the distance between any two vertices in the partial cube is the same as the distance between those vertices in the hypercube. Equivalently, a partial cube is a graph whose vertices can be labeled with bit strings of equal length in such a way that the distance between two vertices in the graph is equal to the Hamming distance between their labels. Such a labeling is called a Hamming labeling; it represents an isometric embedding of the partial cube into a hypercube.
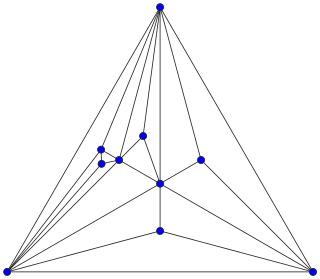
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

In mathematical optimization, the criss-cross algorithm is any of a family of algorithms for linear programming. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints and nonlinear objective functions; there are criss-cross algorithms for linear-fractional programming problems, quadratic-programming problems, and linear complementarity problems.

In mathematics, a flip graph is a graph whose vertices are combinatorial or geometric objects, and whose edges link two of these objects when they can be obtained from one another by an elementary operation called a flip. Flip graphs are special cases of geometric graphs.
Komei Fukuda is a Japanese mathematician known for his contributions to optimization, polyhedral computation and oriented matroid theory. Fukuda is a professor in optimization and computational geometry in the Department of Mathematics and in the Institute of Theoretical Computer Science at ETH Zurich.


















