
In mathematics and more specifically in topology, a homeomorphism, also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.

In mathematics, a Lie group is a group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable.
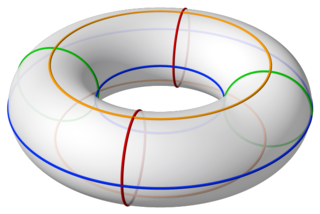
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.

In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology.
In mathematics, more specifically topology, a local homeomorphism is a function between topological spaces that, intuitively, preserves local structure. If is a local homeomorphism, is said to be an étale space over Local homeomorphisms are used in the study of sheaves. Typical examples of local homeomorphisms are covering maps.
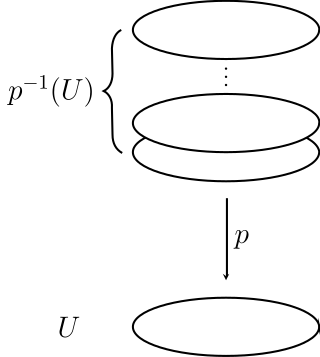
In topology, a covering or covering projection is a map between topological spaces that, intuitively, locally acts like a projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If is a covering, is said to be a covering space or cover of , and is said to be the base of the covering, or simply the base. By abuse of terminology, and may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étale space.

In mathematics, a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable, or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class Cr it is usually understood that r ≥ 1. The number p is called the dimension of the foliation and q = n − p is called its codimension.

In mathematics, the circle group, denoted by or , is the multiplicative group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane or simply the unit complex numbers :|z|=1\}.}
Complex dynamics, or holomorphic dynamics, is the study of dynamical systems obtained by iterating a complex analytic mapping. This article focuses on the case of algebraic dynamics, where a polynomial or rational function is iterated. In geometric terms, that amounts to iterating a mapping from some algebraic variety to itself. The related theory of arithmetic dynamics studies iteration over the rational numbers or the p-adic numbers instead of the complex numbers.

In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower-dimensional subspace, called the Poincaré section, transversal to the flow of the system. More precisely, one considers a periodic orbit with initial conditions within a section of the space, which leaves that section afterwards, and observes the point at which this orbit first returns to the section. One then creates a map to send the first point to the second, hence the name first recurrence map. The transversality of the Poincaré section means that periodic orbits starting on the subspace flow through it and not parallel to it.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.
In mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by small perturbations.

In topology, the degree of a continuous mapping between two compact oriented manifolds of the same dimension is a number that represents the number of times that the domain manifold wraps around the range manifold under the mapping. The degree is always an integer, but may be positive or negative depending on the orientations.

In mathematics, particularly in dynamical systems, Arnold tongues are a pictorial phenomenon that occur when visualizing how the rotation number of a dynamical system, or other related invariant property thereof, changes according to two or more of its parameters. The regions of constant rotation number have been observed, for some dynamical systems, to form geometric shapes that resemble tongues, in which case they are called Arnold tongues.
In mathematics, the Denjoy theorem gives a sufficient condition for a diffeomorphism of the circle to be topologically conjugate to a diffeomorphism of a special kind, namely an irrational rotation. Denjoy proved the theorem in the course of his topological classification of homeomorphisms of the circle. He also gave an example of a C1 diffeomorphism with an irrational rotation number that is not conjugate to a rotation.
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity.
In mathematics, Smale's axiom A defines a class of dynamical systems which have been extensively studied and whose dynamics is relatively well understood. A prominent example is the Smale horseshoe map. The term "axiom A" originates with Stephen Smale. The importance of such systems is demonstrated by the chaotic hypothesis, which states that, 'for all practical purposes', a many-body thermostatted system is approximated by an Anosov system.
In mathematics, two functions are said to be topologically conjugate if there exists a homeomorphism that will conjugate the one into the other. Topological conjugacy, and related-but-distinct § Topological equivalence of flows, are important in the study of iterated functions and more generally dynamical systems, since, if the dynamics of one iterative function can be determined, then that for a topologically conjugate function follows trivially.

In the mathematical theory of dynamical systems, an irrational rotation is a map

In mathematics, especially in the area of mathematical analysis known as dynamical systems theory, a linear flow on the torus is a flow on the n-dimensional torus which is represented by the following differential equations with respect to the standard angular coordinates
























