
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the four known fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different aspects of the same force. Above the unification energy, on the order of 246 GeV, they would merge into a single force. Thus, if the temperature is high enough – approximately 1015 K – then the electromagnetic force and weak force merge into a combined electroweak force. During the quark epoch (shortly after the Big Bang), the electroweak force split into the electromagnetic and weak force. It is thought that the required temperature of 1015 K has not been seen widely throughout the universe since before the quark epoch, and currently the highest human-made temperature in thermal equilibrium is around 5.5x1012 K (from the Large Hadron Collider).

The Fresnel equations describe the reflection and transmission of light when incident on an interface between different optical media. They were deduced by French engineer and physicist Augustin-Jean Fresnel who was the first to understand that light is a transverse wave, when no one realized that the waves were electric and magnetic fields. For the first time, polarization could be understood quantitatively, as Fresnel's equations correctly predicted the differing behaviour of waves of the s and p polarizations incident upon a material interface.
Brightness temperature or radiance temperature is a measure of the intensity of electromagnetic energy coming from a source. In particular, it is the temperature at which a black body would have to be in order to duplicate the observed intensity of a grey body object at a frequency . This concept is used in radio astronomy, planetary science, materials science and climatology.
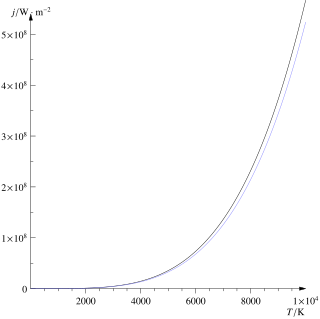
The Stefan–Boltzmann law, also known as Stefan's law, describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically.

In particle physics, bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

A composite material is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a material with properties unlike the individual elements. Within the finished structure, the individual elements remain separate and distinct, distinguishing composites from mixtures and solid solutions.

In physics, Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In radiometry, radiance is the radiant flux emitted, reflected, transmitted or received by a given surface, per unit solid angle per unit projected area. Radiance is used to characterize diffuse emission and reflection of electromagnetic radiation, and to quantify emission of neutrinos and other particles. The SI unit of radiance is the watt per steradian per square metre. It is a directional quantity: the radiance of a surface depends on the direction from which it is being observed.

Black-body radiation is the thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body. It has a specific, continuous spectrum of wavelengths, inversely related to intensity, that depend only on the body's temperature, which is assumed, for the sake of calculations and theory, to be uniform and constant.

An isotropic radiator is a theoretical point source of electromagnetic or sound waves which radiates the same intensity of radiation in all directions. It has no preferred direction of radiation. It radiates uniformly in all directions over a sphere centred on the source. Isotropic radiators are used as reference radiators with which other sources are compared, for example in determining the gain of antennas. A coherent isotropic radiator of electromagnetic waves is theoretically impossible, but incoherent radiators can be built. An isotropic sound radiator is possible because sound is a longitudinal wave.
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission, and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in a wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media, with complex multiple scattering effects, numerical methods are required. The present article is largely focused on the condition of radiative equilibrium.
For most numbered asteroids, almost nothing is known apart from a few physical parameters and orbital elements. Some physical characteristics can only be estimated. The physical data is determined by making certain standard assumptions.

In the mathematical theory of bifurcations, a Hopfbifurcation is a critical point where, as a parameter changes, a system's stability switches and a periodic solution arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system loses stability, as a pair of complex conjugate eigenvalues—of the linearization around the fixed point—crosses the complex plane imaginary axis as a parameter crosses a threshold value. Under reasonably generic assumptions about the dynamical system, the fixed point becomes a small-amplitude limit cycle as the parameter changes.
The method of image charges is a basic problem-solving tool in electrostatics. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem.
The Appleton–Hartree equation, sometimes also referred to as the Appleton–Lassen equation is a mathematical expression that describes the refractive index for electromagnetic wave propagation in a cold magnetized plasma. The Appleton–Hartree equation was developed independently by several different scientists, including Edward Victor Appleton, Douglas Hartree and German radio physicist H. K. Lassen. Lassen's work, completed two years prior to Appleton and five years prior to Hartree, included a more thorough treatment of collisional plasma; but, published only in German, it has not been widely read in the English speaking world of radio physics. Further, regarding the derivation by Appleton, it was noted in the historical study by Gillmor that Wilhelm Altar first calculated the dispersion relation in 1926.
The distortion free energy density is a quantity that describes the increase in the free energy density of a liquid crystal caused by distortions from its uniformly aligned configuration. It also commonly goes by the name Frank free energy density named after Frederick Charles Frank.
With increased interest in sea ice and its effects on the global climate, efficient methods are required to monitor both its extent and exchange processes. Satellite-mounted, microwave radiometers, such SSMI, AMSR and AMSU, are an ideal tool for the task because they can see through cloud cover, and they have frequent, global coverage. A passive microwave instrument detects objects through emitted radiation since different substance have different emission spectra. To detect sea ice more efficiently, there is a need to model these emission processes. The interaction of sea ice with electromagnetic radiation in the microwave range is still not well understood. In general is collected information limited because of the large-scale variability due to the emissivity of sea ice.
The Bowring series of the transverse mercator published in 1989 by Bernard Russel Bowring gave formulas for the Transverse Mercator that are simpler to program but retain millimeter accuracy.
In optics, polarization mixing refers to changes in the relative strengths of the Stokes parameters caused by reflection or scattering—see vector radiative transfer—or by changes in the radial orientation of the detector.





















