Simson line

The Simson line LN (red) of the triangle ABC with respect to point P on the circumcircle

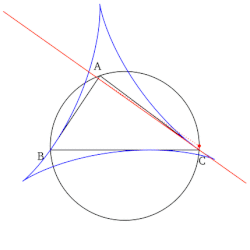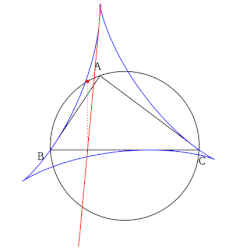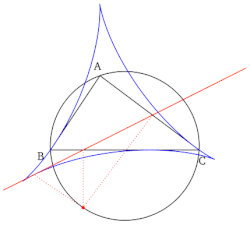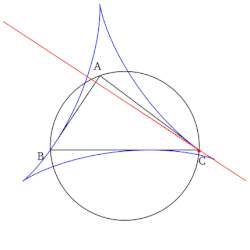
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. ^[1] The line through these points is the Simson line of P, named for Robert Simson. ^[2] The concept was first published, however, by William Wallace in 1799, ^[3] and is sometimes called the Wallace line. ^[4]

The converse is also true; if the three closest points to P on three lines are collinear, and no two of the lines are parallel, then P lies on the circumcircle of the triangle formed by the three lines. Or in other words, the Simson line of a triangle ABC and a point P is just the pedal triangle of ABC and P that has degenerated into a straight line and this condition constrains the locus of P to trace the circumcircle of triangle ABC.

Equation

Placing the triangle in the complex plane, let the triangle ABC with unit circumcircle have vertices whose locations have complex coordinates a, b, c, and let P with complex coordinates p be a point on the circumcircle. The Simson line is the set of points z satisfying ^{[5] : Proposition 4}

${\displaystyle 2abc{\bar {z}}-2pz+p^{2}+(a+b+c)p-(bc+ca+ab)-{\frac {abc}{p}}=0,}$

where an overbar indicates complex conjugation.

Properties

Simson lines (in red) are tangents to the Steiner deltoid (in blue).

• The Simson line of a vertex of the triangle is the altitude of the triangle dropped from that vertex, and the Simson line of the point diametrically opposite to the vertex is the side of the triangle opposite to that vertex.
• If P and Q are points on the circumcircle, then the angle between the Simson lines of P and Q is half the angle of the arc PQ. In particular, if the points are diametrically opposite, their Simson lines are perpendicular and in this case the intersection of the lines lies on the nine-point circle.
• Letting H denote the orthocenter of the triangle ABC, the Simson line of P bisects the segment PH in a point that lies on the nine-point circle.
• Given two triangles with the same circumcircle, the angle between the Simson lines of a point P on the circumcircle for both triangles does not depend of P.
• The set of all Simson lines, when drawn, form an envelope in the shape of a deltoid known as the Steiner deltoid of the reference triangle.
• The construction of the Simson line that coincides with a side of the reference triangle (see first property above) yields a nontrivial point on this side line. This point is the reflection of the foot of the altitude (dropped onto the side line) about the midpoint of the side line being constructed. Furthermore, this point is a tangent point between the side of the reference triangle and its Steiner deltoid.
• A quadrilateral that is not a parallelogram has one and only one pedal point, called the Simson point, with respect to which the feet on the quadrilateral are collinear. ^[6] The Simson point of a trapezoid is the point of intersection of the two nonparallel sides. ^{[7] : p. 186}
• No convex polygon with at least 5 sides has a Simson line. ^[8]

Proof of existence

It suffices to show that ${\displaystyle \angle NMP+\angle PML=180^{\circ }}$.

${\displaystyle PCAB}$ is a cyclic quadrilateral, so ${\displaystyle \angle PBA+\angle ACP=\angle PBN+\angle ACP=180^{\circ }}$. ${\displaystyle PMNB}$ is a cyclic quadrilateral (since ${\displaystyle \angle PMB=\angle PNB=90^{\circ }}$), so ${\displaystyle \angle PBN+\angle NMP=180^{\circ }}$. Hence ${\displaystyle \angle NMP=\angle ACP}$. Now ${\displaystyle PLCM}$ is cyclic, so ${\displaystyle \angle PML=\angle PCL=180^{\circ }-\angle ACP}$.

Therefore ${\displaystyle \angle NMP+\angle PML=\angle ACP+(180^{\circ }-\angle ACP)=180^{\circ }}$.

Generalizations

Generalization 1

The projections of Ap, Bp, Cp onto BC, CA, AB are three collinear points

• Let ABC be a triangle, let a line ℓ go through circumcenter O, and let a point P lie on the circumcircle. Let AP, BP, CP meet ℓ at A_p, B_p, C_p respectively. Let A₀, B₀, C₀ be the projections of A_p, B_p, C_p onto BC, CA, AB, respectively. Then A₀, B₀, C₀ are collinear. Moreover, the new line passes through the midpoint of PH, where H is the orthocenter of ΔABC. If ℓ passes through P, the line coincides with the Simson line. ^{[9] [10] [11]}

A projective version of a Simson line

Generalization 2

• Let the vertices of the triangle ABC lie on the conic Γ, and let Q, P be two points in the plane. Let PA, PB, PC intersect the conic at A₁, B₁, C₁ respectively. QA₁ intersects BC at A₂, QB₁ intersects AC at B₂, and QC₁ intersects AB at C₂. Then the four points A₂, B₂, C₂, and P are collinear if only if Q lies on the conic Γ. ^[12]

Generalization 3

• R. F. Cyster generalized the theorem to cyclic quadrilaterals in The Simson Lines of a Cyclic Quadrilateral

See also

• Pedal triangle
• Robert Simson

References

1. H.S.M. Coxeter and S.L. Greitzer, Geometry revisited, Math. Assoc. America, 1967: p.41.
2. "Gibson History 7 - Robert Simson". MacTutor History of Mathematics archive . 2008-01-30.
3. "William Wallace". MacTutor History of Mathematics archive.
4. Clawson, J. W. (1919). "A Theorem in the Geometry of the Triangle". The American Mathematical Monthly. 26 (2): 59–62. JSTOR   2973140.
5. Todor Zaharinov, "The Simson triangle and its properties", Forum Geometricorum 17 (2017), 373--381. http://forumgeom.fau.edu/FG2017volume17/FG201736.pdf
6. Daniela Ferrarello, Maria Flavia Mammana, and Mario Pennisi, "Pedal Polygons", Forum Geometricorum 13 (2013) 153–164: Theorem 4.
7. Olga Radko and Emmanuel Tsukerman, "The Perpendicular Bisector Construction, the Isoptic point, and the Simson Line of a Quadrilateral", Forum Geometricorum 12 (2012).
8. Tsukerman, Emmanuel (2013). "On Polygons Admitting a Simson Line as Discrete Analogs of Parabolas" (PDF). Forum Geometricorum. 13: 197–208.
9. "A Generalization of Simson Line". Cut-the-knot. April 2015.
10. Nguyen Van Linh (2016), "Another synthetic proof of Dao's generalization of the Simson line theorem" (PDF), Forum Geometricorum, 16: 57–61
11. Nguyen Le Phuoc and Nguyen Chuong Chi (2016). 100.24 A synthetic proof of Dao's generalisation of the Simson line theorem. The Mathematical Gazette, 100, pp 341-345. doi:10.1017/mag.2016.77. The Mathematical Gazette
12. Smith, Geoff (2015), "99.20 A projective Simson line", The Mathematical Gazette, 99 (545): 339–341, doi:10.1017/mag.2015.47, S2CID   124965348

External links

• Simson Line at cut-the-knot.org
• F. M. Jackson and Weisstein, Eric W. "Simson Line". MathWorld .
• A generalization of Neuberg's theorem and the Simson-Wallace line at Dynamic Geometry Sketches, an interactive dynamic geometry sketch.